题目内容
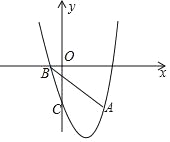
【题目】如图,抛物线y=ax2+bx+c经过点A(2,﹣3),且与x轴交点坐标为(﹣1,0),(3,0)
(1)求抛物线的解析式;
(2)在直线AB下方抛物线上找一点D,求出使得△ABD面积最大时点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
【答案】(1)y=x2-2x-3;(2)当D坐标为(![]() ,-
,-![]() )时,△ABD的面积最大;(3)存在,M点的坐标为(0,-3)、(4,5)、(-2,5).
)时,△ABD的面积最大;(3)存在,M点的坐标为(0,-3)、(4,5)、(-2,5).
【解析】
(1)把交点坐标为(2,-3),(-1,0),(3,0)代入二次函数的表达式,即可求解;
(2)如图,过D点做DF⊥x轴于F,交AB于E,设出D,E点坐标,根据S△ABD=![]() DE×(xA-xB)即可求解;
DE×(xA-xB)即可求解;
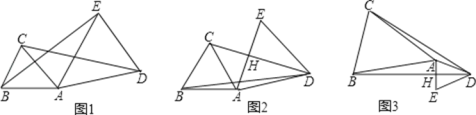
(3)分情况进行讨论,当AB是为平行四边形的边长时,如图所示,M1、M2为所求点;当AB为平行四边形的对角线时,M3与点C重合,即可求解.
(1)把交点坐标为(2,-3),(-1,0),(3,0)代入二次函数的表达式得,
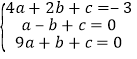 ,
,
解得:a=1,b=-2,c=﹣3,
故二次函数的表达式为:y=x2-2x-3;
(2)如图,过D点做DF⊥x轴于F,交AB于E,
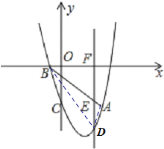
把A(2,-3),B(-1,0)代入一次函数表达式得直线AB的方程为:y=-x-1,
设:D(m,m2-2m-3),E(m,-m-1),
∴DE=-m-1-(m2-2m-3)=-m2+m+2,
S△ABD=![]() DE×(xA-xB)=-
DE×(xA-xB)=-![]() (m-
(m-![]() )2+
)2+![]() ,
,
∴当D坐标为(![]() ,-
,-![]() )时,△ABD的面积最大;
)时,△ABD的面积最大;
(3)当AB是为平行四边形的边长时,
①如图,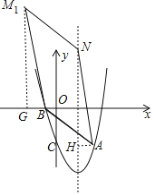
∵四边形ANM1B为平行四边形,
∴△ANH≌△BM1G,
则M1的横坐标为:-2,代入二次函数表达式,
解得:M1坐标为(-2,5);
②如图,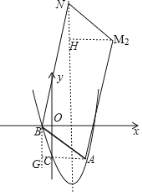
∵四边形ANM2B为平行四边形,
∴△ABG≌△NHM2,
则M2的横坐标为:4,代入二次函数表达式,
解得:M2坐标为(4,5);
当AB时平行四边形的对角线时,如下图所示,
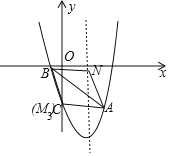
M3与点C重合,
故M3(0,-3);
故M点的坐标为:(0,-3)、(4,5)、(-2,5).