题目内容
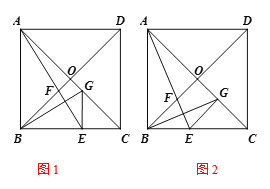
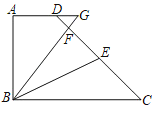
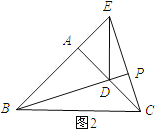
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)直线BD和CE的位置关系是 ;
(2)猜测BD和CE的数量关系并证明;
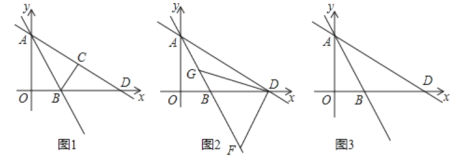
(3)设直线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,直接写出PB的长.

【答案】(1)BD⊥CE;(2)BD=CE,证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据SAS可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到结论;
(2)根据全等三角形的性质即可得到结论;
(3)分为点E在AB上和点E在BA的延长线上两种情况画出图形,然后再证明△BPE∽△BAD,最后依据相似三角形的性质进行证明即可.
解:(1)BD⊥CE,
理由:延长CE交BD于P,
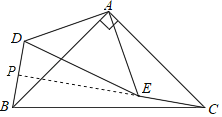
∵将线段AD绕点A逆时针旋转90°,得到线段AE,
∴AD=AE,∠DAE=90°,
∵∠BAC=90°,AB=AC,
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,
∴∠DAB=∠EAC,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,
∵∠ABC+∠ACB=∠ABP+∠ABC+∠PCB=90°,
∴∠BPC=90°,
∴BD⊥CE,
故答案为:BD⊥CE;
(2)BD和CE的数量是:BD=CE;
由(1)知△ABD≌△ACE,
∴BD=CE;
(3)①当点E在AB上时,BE=AB﹣AE=1.
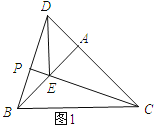
∵∠EAC=90°,
∴CE=![]() =
=![]() ,
,
同(1)可证△ADB≌△AEC.
∵∠AEC=∠BEP,
∴∠BPE=∠EAC=90°,
∵∠PBE=∠ABD,
∴△BPE∽△BAD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BP=![]() .
.
②当点E在BA延长线上时,BE=3,
∵∠EAC=90°,
∴CE=![]() =
=![]() ,
,
由△BPE∽△BAD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PB=![]() ,
,
综上所述,PB的长为![]() 或
或![]() .
.

 快乐小博士巩固与提高系列答案
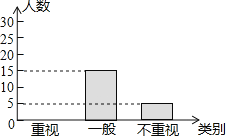
快乐小博士巩固与提高系列答案【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.