题目内容
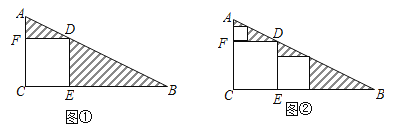
【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
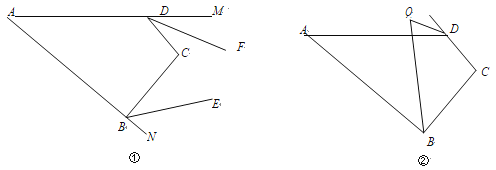
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
【答案】(1)(360-x-y). (2)①30°;x=40,y=80;(3)90+![]() (x-y)
(x-y)
【解析】
(1)利用四边形内角和是360°即可解题,(2)①作出图像,利用四边形的内角和是360°即可解题, ②利用内角和定理和角平分线的性质得到∠PBC+∠PDC=![]() (∠NBC+∠MDC)=
(∠NBC+∠MDC)=![]() (x+y),再延长 BC,与 DP 交于点 Q,利用三角形的外角的性质即可求解,(3)利用四边形BCDQ和四边形ABCD的内角和是360°,分别表示出两个等式,进行化简整理可得∠A+∠ADC+∠C+2∠1=360°,再利用∠1-∠2=90°-(
(x+y),再延长 BC,与 DP 交于点 Q,利用三角形的外角的性质即可求解,(3)利用四边形BCDQ和四边形ABCD的内角和是360°,分别表示出两个等式,进行化简整理可得∠A+∠ADC+∠C+2∠1=360°,再利用∠1-∠2=90°-(![]() )°,即可求解.
)°,即可求解.
解:(1)∵四边形ABCD的内角和是360°,
∴∠ABC+∠ADC=360°-(∠A+∠B)=(360-x-y)°.
(2)①过点C作CH∥DF,
∵ BE∥DF
∴CH∥BE,∠FDC=∠DCH,∠EBC=∠BCH,
∴∠ABC=180°-2∠CBE,∠ADC=180°-2∠FDC,∠BCD=∠EBC+∠FDC,
∴30°+180°-2∠CBE+∠EBC+∠FDC+180°-2∠FDC=360°,
∴∠EBC+∠FDC=30°,即y=30°,

②由(1)得∠ABC+∠ADC =(360-x-y) °
又∵∠ADC+∠MDC=180°,∠ABC+∠NDC=180°
∴∠NBC+∠MDC=(x+y)°
∵BE、DF 分别为平分∠ABC、∠ADC
∴∠PBC=![]() ∠NBC,∠PDC=
∠NBC,∠PDC=![]() ∠MDC
∠MDC
∴∠PBC+∠PDC=![]() (∠NBC+∠MDC)=
(∠NBC+∠MDC)=![]() (x+y)
(x+y)
延长 BC,与 DP 交于点 Q,见下图,
∵∠BCD=∠PDC+∠DQC,∠DQC=∠P+∠QBP(外角性质)
∴∠BCD=∠P+∠PBC+∠PDC
∴y=20+![]() (x+y),即y-x=40
(x+y),即y-x=40
又∵y=2x
∴x=40,y=80
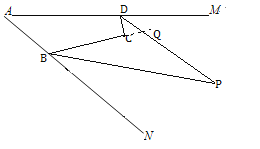
(3)如下图,∵∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,
∴∠ABQ=∠CBQ=∠1,
∵四边形BCDQ和四边形ABCD的内角和是360°,
即∠Q+∠2+∠ADC+∠C+∠1=360°,
∠A+∠ADC+∠C+2∠1=360°,
整理得,∠Q=∠A+(∠1-∠2)
∵∠A+∠ADC+∠C+2∠1=360°,
整理得,∠1-∠2=90°-(![]() )°,
)°,
∴∠Q=[90+![]() (x-y)]°
(x-y)]°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.