Question

【题目】如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG．

（1）求证：△DCG≌△BEG；

（2）你能求出∠BDG的度数吗？若能，请写出计算过程；若不能，请说明理由．

Answer 1

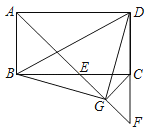
【答案】（1）见解析；（2）∠BDG＝45°，计算过程见解析

【解析】

（1）先求出∠BAE＝45°，判断出△ABE是等腰直角三角形，根据等腰直角三角形的性质可得AB＝BE，∠AEB＝45°，从而得到BE＝CD，再求出△CEF是等腰直角三角形，根据等腰直角三角形的性质可得CG＝EG，再求出∠BEG＝∠DCG＝135°，然后利用“边角边”证明即可．

（2）由△DCG≌△AEG，得出∠DGC＝∠BGE，证出∠BGD＝∠EGC＝90°，即可得出结果．

（1）证明：∵AE平分∠BAD，

∴∠BAE＝45°，

∴△ABE是等腰直角三角形，

∴AB＝BE，∠AEB＝45°，

∵AB＝CD，

∴BE＝CD，

∵∠CEF＝∠AEB＝45°，∠ECF＝90°，

∴△CEF是等腰直角三角形，

∵点G为EF的中点，

∴CG＝EG，∠FCG＝45°，

∴∠BEG＝∠DCG＝135°，

在△DCG和△BEG中，

，

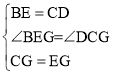∴△DCG≌△BEG（SAS）．

（2）解：∵△DCG≌△BEG，

∴∠DGC＝∠BGE，DG＝BG，

∴∠BGD＝∠EGC＝90°，

∴△BDG等腰直角三角形，

∴∠BDG＝45°．