题目内容
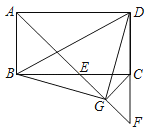
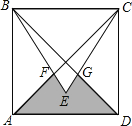
【题目】小芳参加图书馆标志设计大赛,他在边长为2的正方形ABCD内作等边△BCE,并与正方形的对角线交于F、G点,制成了图中阴影部分的标志,则这个标志AFEGD的面积是_____.
【答案】6-3![]()
【解析】
首先过点G作GN⊥CD于N,过点F作FM⊥AB于M,由在边长为2的正方形ABCD内作等边△BCE,即可求得△BEC与正方形ABCD的面积,由直角三角形的性质,即可求得GN的长,即可求得△CDG的面积,同理即可求得△ABF的面积,又由S阴影=S正方形ABCD-S△ABF-S△BCE-S△CDG,即可求得阴影图形的面积.
解:过点G作GN⊥CD于N,过点F作FM⊥AB于M,
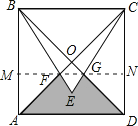
∵在边长为2的正方形ABCD内作等边△BCE,
∴AB=BC=CD=AD=BE=EC=2,∠ECB=60°,∠ODC=45°,
∴S△BEC=![]() ×2×
×2×![]() =
=![]() ,S正方形=AB2=4,
,S正方形=AB2=4,
设GN=x,
∵∠NDG=∠NGD=45°,∠NCG=30°,
∴DN=NG=x,CN=![]() NG=
NG=![]() x,
x,
∴x+![]() x=2,
x=2,
解得:x=![]() ﹣1,
﹣1,
∴S△CGD=![]() CDGN=
CDGN=![]() ×2×(
×2×(![]() ﹣1)=
﹣1)=![]() ﹣1,
﹣1,
同理:S△ABF=![]() ﹣1,
﹣1,
∴S阴影=S正方形ABCD﹣S△ABF﹣S△BCE﹣S△CDG=4﹣(![]() ﹣1)﹣
﹣1)﹣![]() ﹣(
﹣(![]() ﹣1)=/span>6﹣3
﹣1)=/span>6﹣3![]() .
.
故答案为:6﹣3![]() .
.

【题目】某商店销售一种商品,经市场调查发现:该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x、月销售量y、月销售利润w(元)的部分对应值如下表:
售价x(元/件) | 40 | 45 |
月销售量y(件) | 300 | 250 |
月销售利润w(元) | 3000 | 3750 |
注:月销售利润=月销售量×(售价-进价)
(1)①求y关于x的函数表达式;
②当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过40元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2400元,则m的值为 .