题目内容
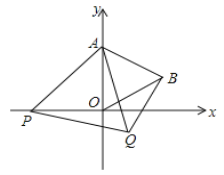
【题目】如图,已知AB=DE,AC=DF,BF=EC

(1)求证:△ABC≌△DEF;
(2)若![]() ,求BF的长;
,求BF的长;
(3)∠B=60°,∠D=70°,求∠AGD.
【答案】(1)见解析;(2)BF= 5;(3)80°
【解析】
(1)已知△ABC与△DEF两边相等,通过BE=CF可得BC=EF,即可判定△ABC≌△DEF(SSS);
(2)已知![]() ,则
,则![]() ,可得
,可得![]() ,利用
,利用![]() ,可求出结果;
,可求出结果;
(3)由△ABC≌△DEF,得∠DFE=∠ACB,通过∠B=60°,∠D=70°,得∠DFE=∠ACB=50°,可求出∠AGD=∠FGC=80°.
证明:(1)∵BF=EC
∴BF+FC=FC+EC
∴BC=EF
∴在△ABC和△DEF中
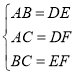
∴△ABC≌△DEF(SSS)
(2)∵![]()
∴![]()
∴![]()
∵BF=EC
∴BF=5
(3)由(1)得:△ABC≌△DEF
∴∠DFE=∠ACB, ∠E =∠B=60°
∵∠D=70°
∴∠DFE=180°-∠E -∠D= 180°-60°-70°= 50°
∴∠DFE=∠ACB=50°
∴∠FGC=180° -(∠DFE+∠ACB)=180°-(50° +50°)=80°
∴∠AGD=∠FGC=80°

练习册系列答案
相关题目
【题目】某中学开展“唱红歌”比赛活动,八年级1、2班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据统计图所给的信息填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | _____ | 85 |
八(2) | _____ | 80 | _____ |
(2)若八(1)班复赛成绩的方差s12=70,请计算八(2)班复赛成绩的方差s22,并说明哪个班级5名选手的复赛成绩更平稳一些.