题目内容
【题目】已知：如图，△ABC中，AB=4，AC=6，AD平分∠BAC，且BD⊥AD于D，交AC于F，E是BC的中点，连接DE．求：DE的长度．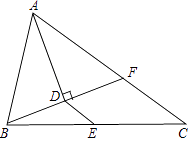 
【答案】解：∵AD平分∠BAC，
∴∠BAD=∠FAD．
∵BD⊥AD于D，
∴∠BDA=∠FDA=90°，
∴△ABF是等腰三角形，
∴AB=AF，BD=FD．
∵AB=4，AC=6，
∴CF=AC﹣AF=6﹣4=2．
∵E是BC的中点，
∴DE= 
CF=1
【解析】先根据题意判断出△ABF是等腰三角形，再由三角形中位线定理即可得出结论．
【考点精析】本题主要考查了三角形中位线定理的相关知识点，需要掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能正确解答此题．
练习册系列答案
习题精选系列答案
相关题目
