Question

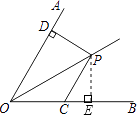
【题目】如图，点P是∠AOB的角平分线上一点，过点P作PC∥OA交OB于点C，PD⊥OA于点D．若OC=5，PD=4，则OP= ．

Answer 1

【答案】4
【解析】解：如图，过点P作PE⊥OB于E，

∵OP是∠AOB的角平分线，PD⊥OA

∴PE=PD=4，

∵OP是∠AOB的角平分线，

∴∠AOP=∠BOP，

∵PC∥OA，

∴∠OPC=∠AOP，

∴∠BOP=∠OPC，

∴PC=OC=5，

在Rt△PCE中，CE= = =3，

∴OE=OC+CE=5+3=8，

在Rt△POE中，OP= = =4 ．

所以答案是：4 ．

【考点精析】认真审题，首先需要了解角平分线的性质定理(定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上)，还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键．