题目内容
已知二次函数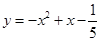 ,当自变量
,当自变量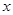 取
取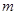 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量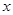 分别取
分别取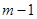 ,
,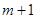 时对应的函数值
时对应的函数值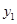 、
、 ,则
,则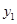 ,
, 满足
满足
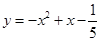 ,当自变量
,当自变量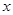 取
取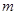 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量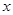 分别取
分别取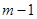 ,
,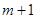 时对应的函数值
时对应的函数值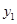 、
、 ,则
,则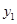 ,
, 满足
满足 A.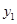 >0, >0, >0 >0 | B.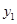 <0, <0, <0 <0 | C.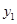 <0, <0, >0 >0 | D.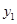 >0, >0, <0 <0 |
B
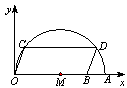
试题分析:根据函数的解析式求得函数与x轴的交点坐标,利用自变量x取m时对应的值大于0,确定m-1、m+1的位置,进而确定函数值为
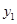 ,
, .
.令
 ,解得
,解得
∵当自变量x取m时对应的值大于0,
∴
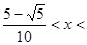

∵点(m+1,0)与(m-1,0)之间的距离为2,大于二次函数与x轴两交点之间的距离,
∴m-1的最大值在左边交点之左,m+1的最小值在右边交点之右.
∴点(m+1,0)与(m-1,0)均在交点之外,
∴
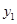 <0,
<0, <0
<0故选B.
点评:此类问题需学生熟练掌握抛物线与x轴的交点和二次函数图象上的点的特征,解题的关键是求得抛物线与横轴的交点坐标.

练习册系列答案
相关题目
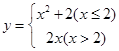 ,则当函数值
,则当函数值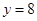 时,自变量
时,自变量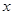 的值是( )
的值是( )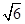
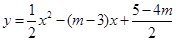 .
. 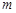 为任何实数,抛物线与
为任何实数,抛物线与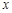 轴总有两个交点;
轴总有两个交点;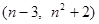 、B
、B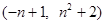 是抛物线上的两个不同点,求抛物线的解析式和
是抛物线上的两个不同点,求抛物线的解析式和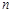 的值;
的值;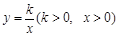 的图象与(2)中的抛物线在第一象限内的交点的横坐标为
的图象与(2)中的抛物线在第一象限内的交点的横坐标为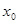 ,且满足2<
,且满足2<
 (百元/m²)
(百元/m²) 与x之间满足的函数关系式;请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出
与x之间满足的函数关系式;请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出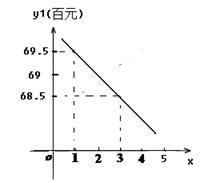
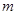 %,楼盘的造价不变,每周的平均销量将比第12周增加5
%,楼盘的造价不变,每周的平均销量将比第12周增加5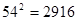 ,
,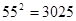 ,
,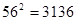 ,
,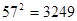 )
) 
 >0.其中正确的结论有( )
>0.其中正确的结论有( )  的图象的对称轴是经过点
的图象的对称轴是经过点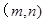 的一条直线,
的一条直线, .
.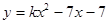 的图象和x轴有交点,则k的取值范围是 ( )
的图象和x轴有交点,则k的取值范围是 ( )