题目内容
如图,在边长为3cm的正方形中,⊙P与⊙Q相外切,且⊙P分别与DA、DC边相切,⊙Q分别与BA、BC边相切,则圆心距PQ为______.

连接BD,则圆心P、Q在BD上,设⊙P与正方形的切点为H、G,设大圆的半径为R,小圆的半径为r,
∵且⊙P分别与DA、DC边相切,
∴PG⊥AD、PH⊥DC,
又∵PG=PH=R,
∴四边形GPHD为正方形,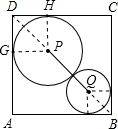
∴DP=
PH=
R,
同理,BQ=
r,
∵AB=AD=3cm,
∴DB=
=3
,
∴DP+PQ+BQ=BD=3
,
即:
r+(r+R)+
R=3
,
∴(
+1)(r+R)=3
,
PQ=
=(6-3
)cm.
故答案为:(6-3
)cm.
∵且⊙P分别与DA、DC边相切,
∴PG⊥AD、PH⊥DC,
又∵PG=PH=R,
∴四边形GPHD为正方形,

∴DP=
| 2 |
| 2 |
同理,BQ=
| 2 |
∵AB=AD=3cm,
∴DB=
| 32+32 |
| 2 |
∴DP+PQ+BQ=BD=3
| 2 |
即:
| 2 |
| 2 |
| 2 |
∴(
| 2 |
| 2 |
PQ=
3
| ||
|
| 2 |
故答案为:(6-3
| 2 |

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目





 O1于D,PC的延长线交⊙O2于A,连接AB,CD,PE.
O1于D,PC的延长线交⊙O2于A,连接AB,CD,PE.