题目内容
如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的大小是（ ）
| A．70° | B．40° | C．50° | D．20° |
连接BC，OB，
∵PA、PB是⊙O的切线，A、B为切点，
∴∠OAP=∠OBP=90°；
而∠P=40°（已知），
∴∠AOB=180°-∠P=140°，
∴∠BOC=40°，
∴∠BAC=
∠BOC=20°（同弧所对的圆周角是所对的圆心角的一半），
故选D．
∵PA、PB是⊙O的切线，A、B为切点，
∴∠OAP=∠OBP=90°；
而∠P=40°（已知），
∴∠AOB=180°-∠P=140°，
∴∠BOC=40°，
∴∠BAC=
| 1 |
| 2 |
故选D．
练习册系列答案
相关题目
=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．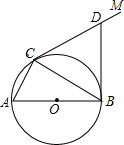
DBC=∠CAB．
