题目内容
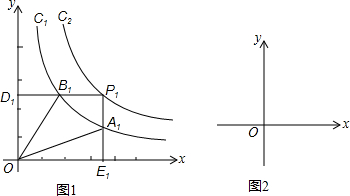
 如图,两个反比例函数y1=
如图,两个反比例函数y1=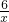 和y=
和y= 在第一象限内的图象一次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为
在第一象限内的图象一次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为
- A.5
- B.6
- C.7
- D.8
A
分析:连接OP,由反比例函数系数k的几何意义可求出△OPC及△OAC的面积,进而可得出△OPA的面积,同理可求出△OPB的面积.进而可得出答案.
解答: 解:连接OP,
解:连接OP,
∴点P在反比例函数y=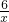 的图象上,
的图象上,
∴S△OPC=S△OPD=3,
∵点A在反比例函数y= 的图象上,
的图象上,
∴S△OAC=S△OBD= ,
,
∴S△OPA=S△OPB=S△OPC-S△OAC=3- =
= ,
,
∴S四边形PAOB=2S△OPA=2× =5.
=5.
故选A.
点评:本题考查的是反比例函数系数k的几何意义,即反比例函数y= (k≠0)图象上的点与坐标轴所围成的三角形的面积为
(k≠0)图象上的点与坐标轴所围成的三角形的面积为 |k|.
|k|.
分析:连接OP,由反比例函数系数k的几何意义可求出△OPC及△OAC的面积,进而可得出△OPA的面积,同理可求出△OPB的面积.进而可得出答案.
解答:
 解:连接OP,
解:连接OP,∴点P在反比例函数y=
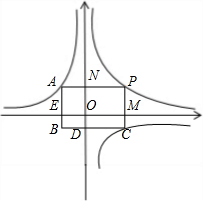
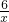 的图象上,
的图象上,∴S△OPC=S△OPD=3,
∵点A在反比例函数y=
 的图象上,
的图象上,∴S△OAC=S△OBD=
 ,
,∴S△OPA=S△OPB=S△OPC-S△OAC=3-
 =
= ,
,∴S四边形PAOB=2S△OPA=2×
 =5.
=5.故选A.
点评:本题考查的是反比例函数系数k的几何意义,即反比例函数y=
 (k≠0)图象上的点与坐标轴所围成的三角形的面积为
(k≠0)图象上的点与坐标轴所围成的三角形的面积为 |k|.
|k|. 
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
 (2012•德州)如图,两个反比例函数
(2012•德州)如图,两个反比例函数 如图,两个反比例函数y=
如图,两个反比例函数y=