题目内容
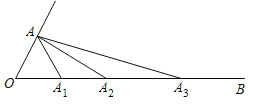
【题目】已知点![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]() (
(![]() 常数)经过点
常数)经过点![]()
(1)求![]() 的解析式及其对称轴和顶点坐标
的解析式及其对称轴和顶点坐标
(2)判断点![]() 是否在
是否在![]() 上,并说明理由;
上,并说明理由;
(3)若线段![]() 以每秒2个单位的速度向下平移,设平移的时间为
以每秒2个单位的速度向下平移,设平移的时间为![]() 秒
秒
①若![]() 与线段
与线段![]() 总有公共点,直接写出
总有公共点,直接写出![]() 的取值范围
的取值范围
②若![]() 同时以每秒3个单位的速度向下平移,
同时以每秒3个单位的速度向下平移,![]() 在
在![]() 轴及其右侧图像与直线
轴及其右侧图像与直线![]() 总有两个公共点,求
总有两个公共点,求![]() 的取值范围.
的取值范围.
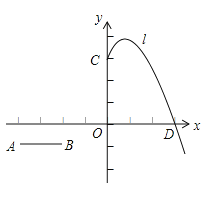
【答案】(1)![]() ,对称轴为
,对称轴为![]() ,顶点坐标为
,顶点坐标为![]() ;(2)不在,理由详见解析;(3)①
;(2)不在,理由详见解析;(3)①![]() ;②
;②![]() .
.
【解析】
(1)直接利用待定系数法求出二次函数即可;
(2)首先得出B点坐标,再代入二次函数解析式进而得出答案;
(3)①分别得出当抛物线G经过点B时,当抛物线G经过点A时,求出y的值,进而得出t的取值范围;
②根据题意得出关于t的不等式进而组成不等式组求出t.
解:(1)把点![]() 的坐标代入
的坐标代入![]() 中,
中,
![]()
得![]() ,
,
∴ 抛物线 G 解析式为![]() =
=![]() ,
,
∴对称轴为![]() ,顶点坐标为
,顶点坐标为![]() ;
;
(2)不在;
∵![]() ,线段
,线段![]() 与
与![]() 轴平行,
轴平行,![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() ,
,
得![]() ,
,
∴ 点![]() 不在抛物线 G上.
不在抛物线 G上.
(3)①设点B的坐标为(-2,-1-2t),则点A的坐标为(-4,-1-2t),
当抛物线G经过点B时,![]() ,
,
当抛物线G经过点A时,![]() ,
,
当抛物线G与线段AB总有公共点时,![]()
解得:![]() .
.
②平移过程中,设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
如果直线![]() 与抛物线
与抛物线![]() 在
在![]() 轴及其右侧的图象总有两个公共点,
轴及其右侧的图象总有两个公共点,
则有![]() ,
,
解得:![]() .
.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.