题目内容
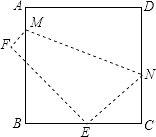
【题目】如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.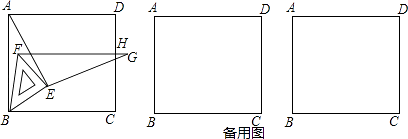
(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求 ![]() 的值.
的值.
【答案】
(1)
证明:在△ABE和△GFE中,
 ,
,
∴△ABE≌△GFE
(2)
解:∵△ABE≌△GFE,
∴∠BAE=∠BGN,
∵∠AMN=∠EMG,
∴∠ANM=∠MEG=90°,
∴MH⊥AB,
同理得,DH=AN,
要使DH最小,则BN最大,
∵BN≤BF,
∴当BF与BN重合时,AN最小,
∴∠ABE=∠FBE=45°
(3)
解:在△APE和△ECG中,
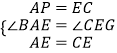 ,
,
∴△APE≌△ECG,
∴GH=BF,
∴∠ECG=APE=135°
∴△HCG是等腰直角三角形,
∴HG=CH=FE,
∴ ![]() ,
,
∵FG=AB=BC,
∴HG=BF,
∴ ![]() .
.
【解析】(1)由等腰直角三角板和正方形ABCD的特点,直接得到△ABE≌△GFE.(2)由△ABE≌△GFE得到的条件判断出MH⊥AB,再判断DH最小时的位置,即可;(3)由△APE≌△ECG得到结论,判断出△HCG是等腰直角三角形,即可求出结果.

练习册系列答案
相关题目