��Ŀ����
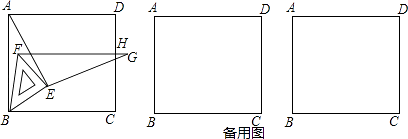
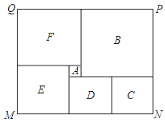
����Ŀ����ͼ�ij�����MNPQ����ij�������㳡��ƽ��ʾ��ͼ��������6��������ƴ�ɵ�(�ֱ���A��B��C��D��E��F������ĸ��ʾ).��֪�м���С��������A�ı߳���1�ף���������C�ı߳���x��.
��1�����ú�x�Ĵ���ʽ�ֱ��ʾ��������EF��B�ı߳���
��2���۲�ͼ�ε��ص㣬�ҳ�����������ϵ���ֱ������ַ����з������x��ֵ��
��3�������ų����ι㳡��������������ˮ�ܵ������ף����������̶ӵ�������ֱ���Ҫ10���15����ɣ�������Ӵ�M����ʼ���ֱ���������ͬ����ͬʱʩ��![]() �����������������µĹ������Ҷӵ���ʩ��10����ɣ���
�����������������µĹ������Ҷӵ���ʩ��10����ɣ���![]() ��ֵ.
��ֵ.
���𰸡���1��E�ı߳�=��x+1������F�ı߳�Ϊ=x+1+1=��x+2������B�ı߳�Ϊ=x+2+1=��x+3����
��2��x=4����3������ͬʱʩ��������Ϊ2��.
�������������������1����ΪC�ı߳���x�ף�����D�ı߳�Ҳ��x�ף�����ΪA�ı߳���1�ף�����E�ı߳�=��x+1���ף�F�ı߳�Ϊ=x+1+1=��x+2���ף�B�ı߳�Ϊ=x+2+1=��x+3���ף���2����PQ=MN��PQ=F�ı߳�+B�ı߳�=x+2+��x+3��=2x+5��MN=E�ı߳�+D�ı߳�+C�ı߳�= x+1+x+x=3x+1����2x+5=3x+1�����x=4����������B�ı߳��ȿ��Ա�ʾΪ��x+3����Ҳ���Ա�ʾΪ��2x��1������x+3=2x��1�����x=4����3���蹤����Ϊ1������������з��̣���![]() +
+![]() ��y+
��y+![]() ��10=1�����y=2.
��10=1�����y=2.
���������
�⣺��1��A�ı߳���1�ף�������C�ı߳���x�ף�
��E�ı߳�=��x+1������
F�ı߳�Ϊ=x+1+1=��x+2������
B�ı߳�Ϊ=x+2+1=��x+3������
��2����PQ=MN��
x+2+��x+3��= x+1+x+x��
x=4��
�������εı߳��ȿ��Ա�ʾΪ��x+3����Ҳ���Ա�ʾΪ��2x��1����
x+3=2x��1��
x=4��
��3���������⣬�г����̣�
![]() ��10=1��
��10=1��
��ã�y=2.
�𣺼���ͬʱʩ��������Ϊ2��.