题目内容
【题目】如图，△ABC是等腰直角三角形，∠A=90°，点P、Q分别是AB、AC上的一动点，且满足BP=AQ，D是BC的中点．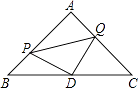 
（1）求证：△PDQ是等腰直角三角形；
（2）当点P运动到什么位置时，四边形APDQ是正方形，并说明理由．
【答案】
（1）证明：连接AD
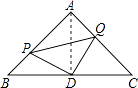
∵△ABC是等腰直角三角形，D是BC的中点
∴AD⊥BC，AD=BD=DC，∠DAQ=∠B，
在△BPD和△AQD中，
，
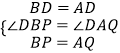∴△BPD≌△AQD（SAS），
∴PD=QD，∠ADQ=∠BDP，
∵∠BDP+∠ADP=90°
∴∠ADP+∠ADQ=90°，即∠PDQ=90°，
∴△PDQ为等腰直角三角形
（2）解：当P点运动到AB的中点时，四边形APDQ是正方形；理由如下：
∵∠BAC=90°，AB=AC，D为BC中点，
∴AD⊥BC，AD=BD=DC，∠B=∠C=45°，
∴△ABD是等腰直角三角形，
当P为AB的中点时，DP⊥AB，即∠APD=90°，
又∵∠A=90°，∠PDQ=90°，
∴四边形APDQ为矩形，
又∵DP=AP= 
AB，
∴矩形APDQ为正方形（邻边相等的矩形为正方形）．
【解析】（1）连接AD，根据直角三角形的性质可得AD=BD=DC，从而证明△BPD≌△AQD，得到PD=QD，∠ADQ=∠BDP，则△PDQ是等腰三角形；由∠BDP+∠ADP=90°，得出∠ADP+∠ADQ=90°，得到△PDQ是直角三角形，从而证出△PDQ是等腰直角三角形；（2）若四边形APDQ是正方形，则DP⊥AP，得到P点是AB的中点．
【考点精析】掌握等腰直角三角形和正方形的判定方法是解答本题的根本，需要知道等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；先判定一个四边形是矩形，再判定出有一组邻边相等；先判定一个四边形是菱形，再判定出有一个角是直角．
