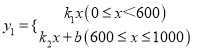题目内容
【题目】王老板经营甲、乙两个服装店铺，每个店铺各在同一段时间内都能售出A、B两种款式的服装合计30件且甲店售1件A款和2件B款可获得110元，售2件A和1件B可获得100元，乙店每售出一件A款获得27元，1件B款获利36元，
（1）问在甲店售出1件A和1件B分别获利多少元？
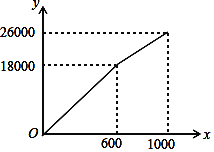
（2）某日王老板进了A款式的服装35件，B款式的服装25件，如果分配给甲店的A款式的服装x件，①求王老板获取的利润y（元）与x（件）之间的函数关系式，并写出x的取值范围；
②由于甲、乙两个店铺所处的地段原因，王老板想在保证乙店利润不小于950元的前提下，使得自己获取的利润最大，请你帮王老板设计一种最佳分配方案，并求最大的总利润是多少？
【答案】（1）在甲店售出1件A和1件B分别获利30元、40元；（2）①
；②最佳分配方案是在甲店出售A种款式的服装21件，B种款式的服装9件，在乙服装店出售A种款式的服装14件，出售B种款式的服装16件，最大的总利润是1944元
【解析】
解：（1）设在甲店售出1件A和1件B分别获利a元、b元，
，得
，
答：在甲店售出1件A和1件B分别获利30元、40元；
（2）①由题意可得，
，
，
，
，
即王老板获取的利润y（元）与x（件）之间的函数关系式是；
②
王老板想在保证乙店利润不小于950元，
，
解得，
，
，
当
时，y取得最大值，此时
，
，
，
，
答：最佳分配方案是在甲店出售A种款式的服装21件，B种款式的服装9件，在乙服装店出售A种款式的服装14件，出售B种款式的服装16件，最大的总利润是1944元．
练习册系列答案
相关题目
