题目内容
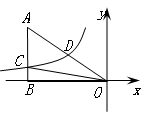
如图，已知双曲线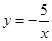
经过Rt△OAB斜边OA的中点D，且与直角边AB相交于点C，△AOC的面积为
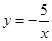经过Rt△OAB斜边OA的中点D，且与直角边AB相交于点C，△AOC的面积为| A．10 | B．7.5 | C．5 | D．2.5 |
B
试题分析：由反比例函数的比例系数k的几何意义，可知△BOC的面积
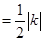，求出k值，由点A的坐标为（2x，2y），根据三角形的面积公式，可知△AOB的面积=10，再利用△AOC的面积=△AOB的面积-△BOC的面积，进而求出即可．∵OA的中点是D，双曲线
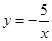经过点D∴
设D点坐标为：（x，y），则A点坐标为：（2x，2y）
∴△BOC的面积
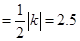
又∵△AOB的面积
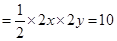
∴△AOC的面积=△AOB的面积-△BOC的面积
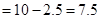
故选B.
点评：解题的关键是熟练掌握一条线段中点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系，即
．
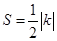练习册系列答案
阅读快车系列答案
相关题目
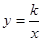的图象经过点（
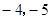），那么这个函数的解析式为（ ）
为反比例函数
图象上一点，长方形
的面积为3，则这个反比例函数解析式为 ． 
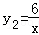的图象都经过点（2，m）．
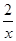(x>0),y=
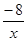(x>0)的图像上且OA⊥OB,则tanB为( )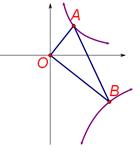 
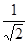
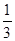
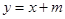与反比例函数
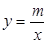的图像在同一平面直角坐标系中是（ ）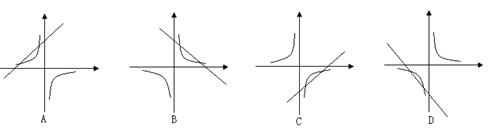
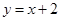与双曲线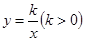
在第一象限内交于点P（a，b），且1.5≤a≤3，则k的取值范围是 ．
x+b与反比例函数y=
的图象交于A(1,6)，B(a,3)两点.
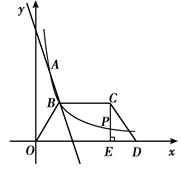
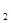的值；
（
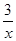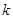为常数，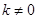
）的图象位于 （ ）