题目内容
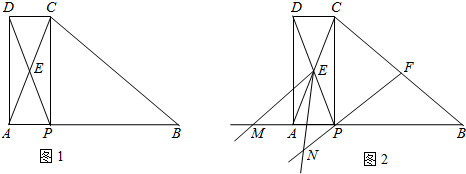
如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作?APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;
(2)?APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
分析:(1)根据AB=BC可证∠CAB=∠ACB,则在△ABC与△AEP中,有两个角对应相等,根据三角形内角和定理,即可证得;
(2)由(1)知∠EPA=∠EAP,则AC=DP,根据对角线相等的平行四边形是矩形即可证明;
(3)可以证明△EAM≌△EPN,从而得到EM=EN.
(2)由(1)知∠EPA=∠EAP,则AC=DP,根据对角线相等的平行四边形是矩形即可证明;
(3)可以证明△EAM≌△EPN,从而得到EM=EN.
解答:(1)证明:在△ABC和△AEP中,
∵∠ABC=∠AEP,∠BAC=∠EAP,
∴∠ACB=∠APE,
在△ABC中,AB=BC,
∴∠ACB=∠BAC,
∴∠EPA=∠EAP.
(2)解:?APCD是矩形.理由如下:
∵四边形APCD是平行四边形,
∴AC=2EA,PD=2EP,
∵由(1)知∠EPA=∠EAP,
∴EA=EP,
则AC=PD,
∴?APCD是矩形.
(3)解:EM=EN.
证明:∵EA=EP,
∴∠EPA=
=
=90°-
α,
∴∠EAM=180°-∠EPA=180°-(90°-
α)=90°+
α,
由(2)知∠CPB=90°,F是BC的中点,
∴FP=FB,
∴∠FPB=∠ABC=α,
∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°-
α+α=90°+
α,
∴∠EAM=∠EPN,
∵∠AEP绕点E顺时针旋转适当的角度,得到∠MEN,
∴∠AEP=∠MEN,
∴∠AEP-∠AEN=∠MEN-∠AEN,即∠MEA=∠NEP,
在△EAM和△EPN中,
∴△EAM≌△EPN(ASA),
∴EM=EN.
∵∠ABC=∠AEP,∠BAC=∠EAP,
∴∠ACB=∠APE,
在△ABC中,AB=BC,
∴∠ACB=∠BAC,
∴∠EPA=∠EAP.
(2)解:?APCD是矩形.理由如下:
∵四边形APCD是平行四边形,
∴AC=2EA,PD=2EP,
∵由(1)知∠EPA=∠EAP,
∴EA=EP,
则AC=PD,
∴?APCD是矩形.
(3)解:EM=EN.
证明:∵EA=EP,
∴∠EPA=
| 180°-∠AEP |
| 2 |
| 180°-∠ABC |
| 2 |
| 1 |
| 2 |
∴∠EAM=180°-∠EPA=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
由(2)知∠CPB=90°,F是BC的中点,
∴FP=FB,
∴∠FPB=∠ABC=α,
∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAM=∠EPN,
∵∠AEP绕点E顺时针旋转适当的角度,得到∠MEN,
∴∠AEP=∠MEN,
∴∠AEP-∠AEN=∠MEN-∠AEN,即∠MEA=∠NEP,
在△EAM和△EPN中,
|
∴△EAM≌△EPN(ASA),
∴EM=EN.
点评:本题主要考查了等腰三角形的性质,以及矩形的判定方法,在旋转中找到题目中存在的相等的线段以及相等的角是解决本题的关键.

练习册系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=