题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形. 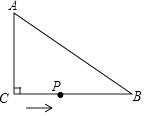
【答案】3或6或6.5或5.4
【解析】解:∵AC=6,BC=8, ∴由勾股定理可知:AB=10,
当点P在CB上运动时,
由于∠ACP=90°,
∴只能有AC=CP,如图1,
∴CP=6,
∴t= ![]() =3,
=3,
当点P在AB上运动时,①AC=AP时,如图2,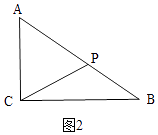
∴AP=6,PB=AB﹣CP=10﹣6=4,
∴t= ![]() =6,②当AP=CP时,如图3,
=6,②当AP=CP时,如图3,
此时点P在线段AC的垂直平分线上,
过点P作PD⊥AC于点D,
∴CD= ![]() AC=3,PD是△ACB的中位线,
AC=3,PD是△ACB的中位线,
∴PD= ![]() BC=4,
BC=4,
∴由勾股定理可知:AP=5,
∴PB=5,
∴t= ![]() =6.5;③AC=PC时,如图4,
=6.5;③AC=PC时,如图4,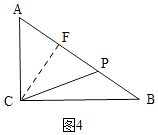
过点C作CF⊥AB于点F,
∴cos∠A= ![]() =
= ![]() ,
,
∴AF=3.6,
∴AP=2AF=7.2,
∴PB=10﹣7.2=2.8,
∴t= ![]() =5.4;
=5.4;
综上所述,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
故答案为:3或6或6.5或5.4.
由于没有说明哪一条边是腰,故需要分情况讨论.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目