题目内容
【题目】已知一次函数y1＝kx＋b的图像经过点（0，-2），（2，2）.
（1）求一次函数的表达式，并在所给直角坐标系中画出此函数的图像；；
（2）根据图像回答：当x 时，y1=0；
（3）求直线y1＝kx＋b、直线y2＝-2x+4与y轴围成的三角形的面积．
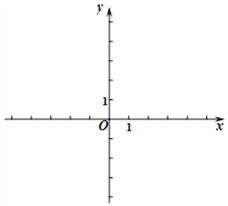
【答案】（1）y＝2x-2 （2）x=1 （3）
【解析】试题分析：（1）利用待定系数法将坐标代入解析式，解方程组即可得解析式，经过给的两点即可画出函数的图象；
（2）观察图象即可得；
（3）求出两个函数图象的交点，两函数图象与y轴的交点，然后利用三角形面积公式即可得.
试题解析：（1）由一次函数y1＝kx＋b的图像经过点（0，-2），（2，2），则有
，解得： 
，所以解析式为：y＝2x-2，
图象如图所示；
（2）观察图象可知当y=0时，x=1，
故答案为：1；
（3）由直线y2＝-2x+4与y轴将于点B，所以B（0，4），由A（0，-2），所以AB=6，
解方程组
， 得
，所以C（1.5，1）
所以S=
=
.
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
