题目内容
已知二次函数y=x2–kx+k–1(k>2).
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与 相离、相切、相交.
相离、相切、相交.
(1)证明见解析;
(2)抛物线的表达式为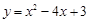 ;
;
(3)当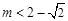 或
或 时,x轴与
时,x轴与 相离.
相离.
当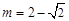 或
或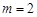 或
或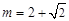 时,x轴与
时,x轴与 相切.
相切.
当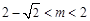 或
或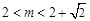 时,x轴与
时,x轴与 相交.
相交.
解析试题分析:(1)要证明二次函数的图象与x轴都有两个交点,证明二次函数的判别式是正数即可解决问题;
(2)根据函数解析式求出A、B、C点坐标,再由 ,求出函数解析式;
,求出函数解析式;
(3)先求出当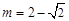 或
或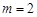 或
或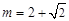 时,x轴与
时,x轴与 相切,再写出相离与相交.
相切,再写出相离与相交.
试题解析:(1)∵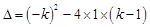
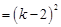 ,
,
又∵ ,
,
∴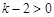 .
.
∴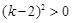 即
即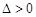 .
.
∴抛物线y=x2–kx+k-1与x轴必有两个交点;
(2)∵抛物线y=x2–kx+k-1与x轴交于A、B两点,
∴令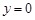 ,有
,有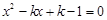 .
.
解得: .
.
∵ ,点A在点B的左侧,
,点A在点B的左侧,
∴ .
.
∵抛物线与y轴交于点C,
∴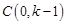 .
.
∵在Rt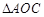 中,
中, ,
,
∴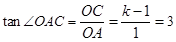 ,解得
,解得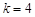 .
.
∴抛物线的表达式为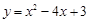 ;
;
(3)解:当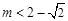 或
或 时,x轴与
时,x轴与 相离.
相离.
当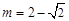 或
或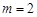 或
或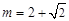 时,x轴与
时,x轴与 相切.
相切.
当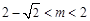 或
或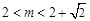 时,x轴与
时,x轴与 相交.
相交.
考点:二次函数综合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D.
中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D. 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿 轴正方向移动.设移动时间为
轴正方向移动.设移动时间为 秒.
秒.
 (x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少? 轴于点
轴于点 ,交
,交 轴于
轴于 ,
, 两点(点
两点(点
 的垂线交抛物线于点
的垂线交抛物线于点 ,如果以点
,如果以点 相切,先补全图形,再判断直线
相切,先补全图形,再判断直线 与⊙
与⊙ 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 的面积最大?求出
的面积最大?求出