Question

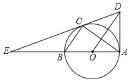
【题目】如图，AB是⊙O直径，C是半圆上一点，连接BC、AC，过点O作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．

（1）求证：DE是⊙O的切线；

（2）若AE=3，CE=，求线段CE、BE与劣弧BC所围成的图形面积（结果保留根号和π）．

Answer 1

【答案】(1)见解析;(2) ﹣．

【解析】

（1）如图，连接OC．欲证DE是⊙O的切线，只需证得OC⊥DE；

（2）设AD=CD=x，Rt△ADE中，由AD2+AE2=DE2求得x的值，从而得出DE=2AD，据此知∠E=30°、∠BOC=60°，设圆的半径为r，在Rt△OCE中由OC2+CE2=OE2可得r的值，根据S=S△COE-S扇形BOC求解可得．

（1）如图，连接OC，

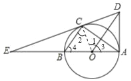
∵AD是过点A的切线，AB是⊙O的直径，

∴AD⊥AB，

∴∠DAB=90°．

∵OD∥BC，

∴∠1=∠2，∠3=∠4．

∵OC=OB，

∴∠2=∠4．

∴∠1=∠3．

在△COD和△AOD中，

∵

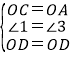
∴△COD≌△AOD（SAS）

∴∠OCD=∠DAB=90°，即OC⊥DE于点C．

∵OC是⊙O的半径，

∴DE是⊙O的切线；

（2）设AD=x，

由△COD≌△AOD知CD=AD=x，

在Rt△ADE中，由AD2+AE2=DE2可得x2+32=（+x）2，

解得：x=，

则AD=、DE=2，

∴sin∠E=，

∴∠E=30°，

∵∠ACE=90°，

∴∠COB=60°，

设圆的半径为r，

在Rt△OCE中，由OC2+CE2=OE2可得r2+（）2=（3﹣r）2，

解得：r=1，

则S=S△COE﹣S扇形BOC=．