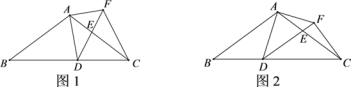题目内容
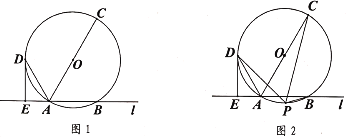
【题目】如图1,直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,连结
,连结![]() ,且
,且![]() 平分
平分![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
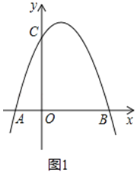
(3)如图2,在(2)的条件下,点![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,
,![]() ,问:线段
,问:线段![]() ,
,![]() ,
,![]() 之间存在什么数量关系?请说明理由.
之间存在什么数量关系?请说明理由.
【答案】(1)证明见解析;(2)![]() 的半径为
的半径为![]() ;(3)
;(3)![]() .
.
【解析】
(1)由OA=OD得∠OAD=∠ODA,由AD平分∠CAM得∠OAD=∠DAE,则∠ODA=∠DAE,所以DO∥AB,利用DE⊥AB得到DE⊥OD,然后根据切线的判定定理即可得到结论;
(2)连结DC,先利用勾股定理计算出AD长,由AC是⊙O直径得到∠ADC=90°,易证得△ACD∽△ADE,利用相似比可计算出AC,即可得到圆的半径;
(3)可得结论PC=PD+PB,连接PB、DB,在CP上截取PB=PF,连接BF、BC,可证△PBF为等边三角形,再证△PBD≌△FBC,即可得结论.
解:(1)连结![]() ,如图,
,如图,
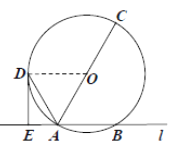
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)∵![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
连结![]() ,
,
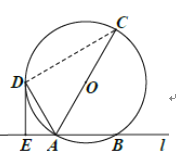
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() .
.
∴![]() 的半径为
的半径为![]() .
.
(3)![]() .
.
理由:连接![]() 、
、![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,
,
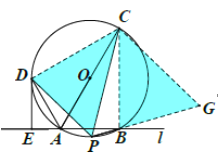
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 内接于
内接于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目