题目内容
【题目】在平面直角坐标系xOy中,直线y=kx+2k(k>0)与x轴交于点P,与双曲线![]() (x>0)交于点Q,若直线y=4kx-2与直线PQ交于点R(点R在点Q右侧),当RQ≤PQ时,k的取值范围是__.
(x>0)交于点Q,若直线y=4kx-2与直线PQ交于点R(点R在点Q右侧),当RQ≤PQ时,k的取值范围是__.
【答案】0<k≤5
【解析】
由直线y=kx+2k(k>0)求得点P的坐标,作QM⊥x轴于M,RN⊥x轴于N,根据平行线分线段成比例定理得到![]() =
=![]() ,即可得到MN≤PM,联立方程求得交点Q,R的横坐标,即可求得M、N的坐标,进一步求得PM、MN的长,即可得到
,即可得到MN≤PM,联立方程求得交点Q,R的横坐标,即可求得M、N的坐标,进一步求得PM、MN的长,即可得到![]() -1≤3,解不等式即可求得k的取值范围.
-1≤3,解不等式即可求得k的取值范围.
解:如图,作QM⊥x轴于M,RN⊥x轴于N,
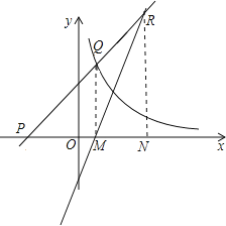
∴QM∥RN,
∴![]() =
=![]() ,
,
∵RQ≤PQ,
∴MN≤PM,
∵直线y=kx+2k(k>0)与x轴交于点P,
∴P(-2,0),
∴OP=2,
解kx+2k=![]() 得,x1=-3,x2=1,
得,x1=-3,x2=1,
∴Q点的横坐标为1,
∴M(1,0),
∴OM=1,
∴PM=2+1=3,
解kx+2k=4kx-2得,x=![]() ,
,
∴R的横坐标为![]() ,
,
∴N(![]() ,0),
,0),
∴ON=![]() ,
,
∴MN=![]() -1,
-1,
∴![]() -1≤3,
-1≤3,
解得k≤5,
故答案为0<k≤5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目