Question

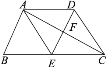
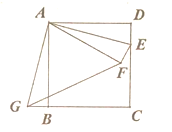
【题目】如图，正方形的边长为4，点在的边上，且，与关于所在的直线对称，将按顺时针方向绕点旋转得到，连接，则线段的长为（ ）

A.4B.C.5D.6

Answer 1

【答案】C

【解析】

如图，连接BE，根据轴对称的性质得到AF=AD，∠EAD=∠EAF，根据旋转的性质得到AG=AE，∠GAB=∠EAD．求得∠GAB=∠EAF，根据全等三角形的性质得到FG=BE，根据正方形的性质得到BC=CD=AB=4．根据勾股定理即可得到结论．

解：如图，连接BE，

∵△AFE与△ADE关于AE所在的直线对称，

∴AF=AD，∠EAD=∠EAF，

∵△ADE按顺时针方向绕点A旋转90°得到△ABG，

∴AG=AE，∠GAB=∠EAD．

∴∠GAB=∠EAF，

∴∠GAB+∠BAF=∠BAF+∠EAF．

∴∠GAF=∠EAB．

∴△GAF≌△EAB（SAS）．

∴FG=BE，

∵四边形ABCD是正方形，

∴BC=CD=AB=4．

∵DE=1，

∴CE=3．

∴在Rt△BCE中，BE=，

∴FG=5，

故选：C．