题目内容
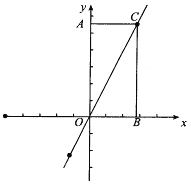
【题目】在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港,设甲乙两船行驶的时间为x(h),与B港的距离为y(km),它们间的函数关系如图所示,若两船的距离不超过10km时能够相互望见,则甲乙两船可以互相望见的时间共有小时.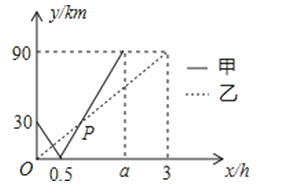
【答案】1
【解析】解:由图象可知,
甲船的速度为:30÷0.5=60千米/时,
乙船的速度为:90÷3=30千米/时,
由此可得:
所以,甲、乙两船离A港口的距离为S甲=60x,S乙=30x+30,
①当乙船在甲船前面10千米时,S乙﹣S甲=10,
即:30x+30﹣60x=10,解得x=![]() ,
,
②当甲船在乙船前面10千米时,S甲﹣S乙=10,
即:60x﹣(30x+30)=10,解得x=![]() ,
,
所以,当![]() ≤x≤
≤x≤![]() 时,甲、乙两船可以相互望见;
时,甲、乙两船可以相互望见;
③由图可知,A、B两港相距30km,B、C两港相距90km,A、C两港相距120km,
甲船到达C港需要的时间:120÷60=2小时,乙船到达C港需要的时间:90÷30=3小时,
当2≤x≤3时,甲船已经到了而乙船正在行驶,
两船的距离是10km,即乙船与C港的距离是10km,
即:120﹣(30x+30)=10,解得x=![]() ,
,
所以,当![]() ≤x≤3时,甲、乙两船可以相互望见;
≤x≤3时,甲、乙两船可以相互望见;
(![]() ﹣
﹣![]() )+(3﹣
)+(3﹣![]() )=1小时.
)=1小时.
所以答案是1.

练习册系列答案
相关题目