��Ŀ����
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ�Rt��ABC�Ķ�����ڸ���ϣ�����ƽ��ֱ������ϵ��A������Ϊ����4��1������C������Ϊ����1��1������Rt��ABC��һ���Ĺ��ɱ任����һ�Σ���Rt��ABC��AC�߷��ۣ���Rt��AB1C���ڶ��Σ���Rt��AB1C�Ƶ�B1��ʱ����ת90�㣬��Rt��A1B1C1�������Σ���Rt��A1B1C1��A1C1�߷��ۣ���Rt��A1B2C1�����ĴΣ���Rt��A1B2C1�Ƶ�B2��ʱ��90�㣬��Rt��A2B2C2�����������ȥ
��1������ͼ�л���Rt��A1B1C1��Rt��A2B2C2 �� ��д��A1������ ��
��2����ֱ��д���ڵ�11�α任�����õĵ�B�Ķ�Ӧ�ĵ�������� ��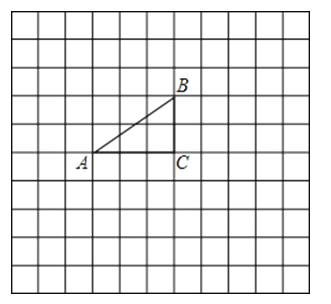
���𰸡�����3����4��������5����1��
���������⣺��1����ͼ��Rt��A1B1C1��Rt��A2B2C2Ϊ������A1������Ϊ����3����4����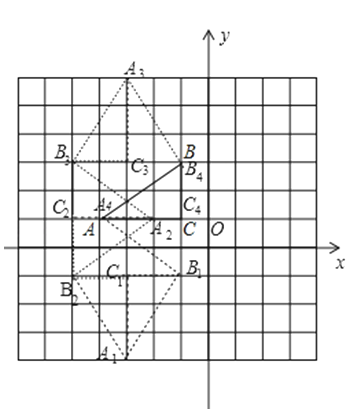
��2����8�α任�����á�A4B4C4���ABC�غϣ�
���Ե�11�α任������������A1B2C1�غϣ�
�������õĵ�B�Ķ�Ӧ�ĵ������Ϊ����5����1����
���Դ��ǣ���3����4��������5����1����

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ