题目内容
如图．在△ABC中．D是AB的中点．E是CD的中点．过点C作CF∥AB交AE的延长线于点F．连结BF。
（1）求证：DB=CF；
（2）在△ABC中添加一个条件： ，使四边形BDCF为 （填：矩形或菱形）。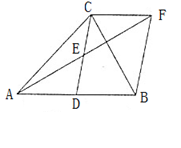
（1）求证：DB=CF；
（2）在△ABC中添加一个条件： ，使四边形BDCF为 （填：矩形或菱形）。
（1）证明：∵CF∥AB，∴∠EAD=∠CFE，∠AED=∠CEF，∵E是CD的中点，∴CE=DE，∴△BCD≌△CEB（AAS），∴AD=CF，
∵D是AB的中点，∴AD=BD，∴BD = CF。
（2）AC=BC，矩形；或 ∠ACB=90°，菱形。
∵D是AB的中点，∴AD=BD，∴BD = CF。
（2）AC=BC，矩形；或 ∠ACB=90°，菱形。
（1）根据CF∥AB，可知∠DAE=∠CFE，得出△ADE≌△FCE，再根据等量代换可知DB=CF，
（2）根据DB=CF，DB∥CF，可知四边形BDCF为平行四边形，再根据AC=BC，AD=DB，得出四边形BDCF是矩形．
（2）根据DB=CF，DB∥CF，可知四边形BDCF为平行四边形，再根据AC=BC，AD=DB，得出四边形BDCF是矩形．
练习册系列答案
相关题目
中，
且
，
、
分别是两底的中点，连结
，若
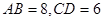，求
