题目内容
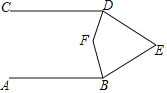
【题目】如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
【答案】(1)270°;(2)DB2=DA2+DC2;(3)![]() .
.
【解析】
(1)利用四边形内角和定理计算即可;
(2)连接BD.以BD为边向下作等边三角形△BDQ.想办法证明△DCQ是直角三角形即可解决问题;
(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.想办法证明∠BEC=150°即可解决问题.
(1)如图1中,
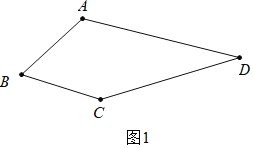
在四边形ABCD中,
∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠C=30°,
∴∠A+∠C=360°﹣60°﹣30°=270°;
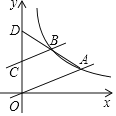
(2)如图2中,结论:DB2=DA2+DC2,
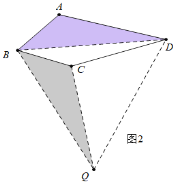
理由:连接BD,以BD为边向下作等边三角形△BDQ,
∵∠ABC=∠DBQ=60°,
∴∠ABD=∠CBQ,
∵AB=BC,DB=BQ,
∴△ABD≌△CBQ,
∴AD=CQ,∠A=∠BCQ,
∵∠A+∠BCD=∠BCQ+∠BCD=270°,
∴∠DCQ=90°,
∴DQ2=DC2+CQ2,
∵CQ=DA,DQ=DB,
∴DB2=DA2+DC2;
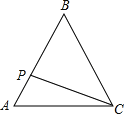
(3)如图3中,
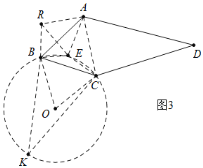
连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE,则△AER是等边三角形,
∵EA2=EB2+EC2,EA=RE,EC=RB,
∴RE2=RB2+EB2,
∴∠EBR=90°,
∴∠RAE+∠RBE=150°,
∴∠ARB+∠AEB=∠AEC+∠AEB=210°,
∴∠BEC=150°,
∴点E的运动轨迹在O为圆心的圆上,在⊙O上取一点K,连接KB,KC,OB,OC,
∵∠K+∠BEC=180°,
∴∠K=30°,∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴点E的运动路径![]() .
.

 应用题作业本系列答案
应用题作业本系列答案