题目内容
【题目】已知△ABC是等腰直角三角形,AB=AC,D为平面内的任意一点,且满足CD=AC,若△ADB是以AD为腰的等腰三角形,则∠CDB的度数为_____.
【答案】45°或135°.
【解析】
当△ADB是以AD为腰的等腰三角形,可以分两种情况进行讨论:①AD=AB,②AD=BD;
①当AD=AB时,又分两种情况:
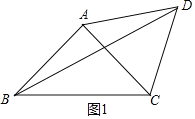
当点D在AC边上方时,如图1所示.由△ACD为等边三角形,得∠CAD=60°,根据角的关系可得结论;
当点D在AC边下方时,如图2所示.同理可得结论;
②当AD=BD时又分两种情况:
当点D在BC的上方,如图3所示.作辅助线,证明∠EDA=∠ADC,根据角平分线的性质得:AF=AE=![]() AB=
AB=![]() AC,利用直角三角形30°角的判定得:Rt△AFC中,∠ACF=30°,从而得出结论;
AC,利用直角三角形30°角的判定得:Rt△AFC中,∠ACF=30°,从而得出结论;
当D在BC的下方时,如图4,同理构建矩形AEFC,由CF=![]() AB=
AB=![]() AC=
AC=![]() CD,得Rt△CFD中,∠CDF=30°,可得结论.
CD,得Rt△CFD中,∠CDF=30°,可得结论.
解:①当AD=AB时,
∵AB=AC,CD=AC,AD=AB,
∴AC=AD=CD,
∴△ACD为等边三角形.
当点D在AC边上方时,如图1所示.
∵△ABC是等腰直角三角形,AB=AC,△ACD为等边三角形,
∴∠BAC=90°,∠CAD=60°,
∴∠BAD=∠BAC+∠CAD=150°.
∵AB=AD,
∴∠ABD=∠ADB=![]() (180°﹣∠BAD)=15°,
(180°﹣∠BAD)=15°,
∴∠CDB=∠ADC﹣∠ADB=60°﹣15°=45°;
当点D在AC边下方时,如图2所示.
∵∠BAC=90°,∠CAD=60°,
∴∠BAD=∠BAC﹣∠CAD=30°.
∵AB=AD,
∴∠ABD=∠ADB=![]() (180°﹣∠BAD)=75°,
(180°﹣∠BAD)=75°,
∴∠CDB=∠ADB+∠ADC=75°+60°=135°.
②当AD=BD时,
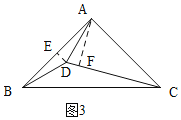
当点D在BC的上方,如图3所示.
过D作DE⊥AB于E,过A作AF⊥CD于F,
∴∠BED=90°,
∵∠BAC=90°,
∴∠BED=∠BAC,
∴ED∥AC,
∴∠EDA=∠DAC,
∵AD=CD,
∴∠ADC=∠DAC,
∴∠EDA=∠ADC,
∴AF=AE=![]() AB=
AB=![]() AC,
AC,
Rt△AFC中,∠ACF=30°,
∴∠ADC=![]() =75°,
=75°,
∴∠ADB=2∠ADE=2∠ADC=150°,
∴∠CDB=360°﹣150°﹣75°=135°;
当D在BC的下方时,如图4,
过D作DE⊥AC于E,过C作CF⊥ED于F,
∴∠AEF=∠BAC=∠EFC=90°,
∴四边形AEFC是矩形,
∴CF=AE,
∵AD=BD,DE⊥AB,
∴AE=![]() AB,∠ADE=∠BDE,
AB,∠ADE=∠BDE,
∴CF=![]() AB=
AB=![]() AC=
AC=![]() CD,
CD,
Rt△CFD中,∠CDF=30°,
∵AC∥ED,
∴∠CAD=∠ADE,
∵AC=CD,
∴∠CAD=∠ADC,
∴∠CDA=∠ADE=![]() ∠CDF=15°,
∠CDF=15°,
∴∠ADB=30°,
∴∠CDB=45°.
综上所述,则∠CDB的度数为45°或135°;
故答案为:45°或135°.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】如图,矩形ABCD中,AB=6,AD=4![]() ,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.
,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.

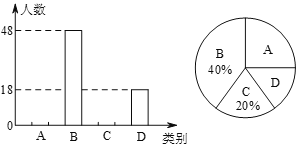
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.