题目内容
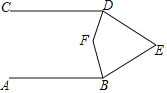
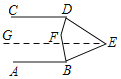
【题目】如图，AB∥CD，∠BED＝60°，∠ABE的角平分线与∠CDE的角平分线交于点F，则∠DFB＝（ ）
A. 150°B. 120°C. 100°D. 135°
【答案】A
【解析】
过点E作EG∥AB，根据平行线的性质可得“∠ABE+∠BEG＝180°，∠GED+∠EDC＝180°”，根据角的计算以及角平分线的定义可得“∠FBE+∠EDF＝
（∠ABE+∠CDE）”，再依据四边形内角和为360°结合角的计算即可得出结论．
如图，过点E作EG∥AB，
∵AB∥CD，
∴AB∥CD∥GE，
∴∠ABE+∠BEG＝180°，∠GED+∠EDC＝180°，
∴∠ABE+∠CDE+∠BED＝360°；
又∵∠BED＝60°，
∴∠ABE+∠CDE＝300°．
∵∠ABE和∠CDE的平分线相交于F，
∴∠FBE+∠EDF＝（∠ABE+∠CDE）＝150°，
∵四边形的BFDE的内角和为360°，
∴∠BFD＝360°﹣150°﹣60°＝150°．
故选：A．
【题目】小王是“新星厂”的一名工人，请你阅读下列信息：
信息一：工人工作时间：每天上午8：00—12：00，下午14：00—18：00，每月工作25天；
信息二：小王生产甲、乙两种产品的件数与所用时间的关系见下表：
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三：按件计酬，每生产一件甲种产品得1.50元，每生产一件乙种产品得2.80元；
信息四：该厂工人每月收入由底薪和计酬工资两部分构成，小王每月的底薪为1900元．请根据以上信息，解答下列问题：
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟；
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件，则小王该月收入最多是多少元？此时小王生产的甲、乙两种产品分别是多少件？
