题目内容
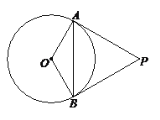
【题目】如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以点P为圆心,3为半径作⊙P,连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由.

【答案】⊙P与x轴相切.
【解析】
由直线y=-2x-8可求出A、B的坐标从而求出OA、OB的长,再结合点P的坐标表示出AP的长,然后在Rt△AOP中,利用勾股定理列方程求解即可.
解:⊙P与x轴相切,
理由:直线y=-2x-8与x轴交于A(-4,0),与y轴交于B(0,-8),
∴OA=4,OB=8,由题意OP=-k,
∴PB=PA=8+k,在Rt△AOP中,k2+42=(8+k)2,
∴k=-3,
∴OP等于⊙P的半径,
∴⊙P与x轴相切

练习册系列答案
相关题目
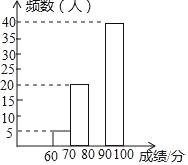
【题目】某校组织了一次全校2000名学生参加的比赛,赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(成绩x取整数,满分100分)作为样本进行整理,得到下列不完整的统计表:
请依据所给信息,解答下列问题:
(1)直接填空:a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)请自己提出一个与该题信息相关的问题,并解答你提出的问题.
成绩x/分 | 频数 | 频率 |
60≤x<70 | 5 | 0.05 |
70≤x<80 | 20 | b |
80≤x<90 | a | c |
90≤x≤100 | 40 | 0.40 |