题目内容
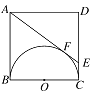
【题目】如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积为_______.
【答案】6cm2
【解析】
由于AE与圆O切于点F,根据切线长定理有AF=AB=4cm,EF=EC;设EF=EC=xcm.则DE=(4-x)cm,AE=(4+x)cm, 然后在三角形BCE中由勾股定理可以列出关于x的方程,解方程即可求出,然后就可以求出△ADE的面积.
∵AE与圆O切于点F,
显然根据切线长定理有AF=AB=4cm,EF=EC,
设EF=EC=xcm,
则DE=(4-x)cm,AE=(4+x)cm,
在三角形ADE中由勾股定理得:
(4-x)2+42=(4+x)2,
∴x=1cm,
∴CE=1cm,
∴DE=4-1=3cm,
∴S△ADE=ADDE÷2=3×4÷2=6(cm2).
故答案为:6cm2

练习册系列答案
相关题目