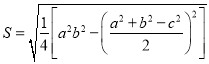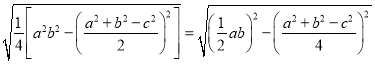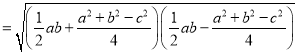题目内容
【题目】（（2016北京市）在平面直角坐标系xOy中，点P的坐标为（
，
），点Q的坐标为（
，
），且
，
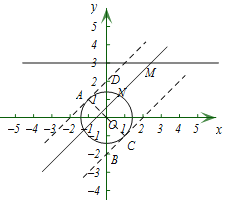
，若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．下图为点P，Q 的“相关矩形”的示意图．
（1）已知点A的坐标为（1，0）．
①若点B的坐标为（3，1）求点A，B的“相关矩形”的面积；
②点C在直线x=3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；
（2）⊙O的半径为
，点M的坐标为（m，3）．若在⊙O上存在一点N，使得点M，N的“相关矩形”为正方形，求m的取值范围．
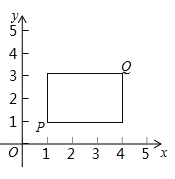
【答案】（1）①2；②
或 
；（2）1≤m≤5 或者
．
【解析】
试题分析：（1）①由相关矩形的定义可知：要求A与B的相关矩形面积，则AB必为对角线，利用A、B两点的坐标即可求出该矩形的底与高的长度，进而可求出该矩形的面积；
②由定义可知，AC必为正方形的对角线，所以AC与x轴的夹角必为45，设直线AC的解析式为；y=kx+b，由此可知k=±1，再（1，0）代入y=kx+b，即可求出b的值；
（2）由定义可知，MN必为相关矩形的对角线，若该相关矩形的为正方形，即直线MN与x轴的夹角为45°，由因为点N在圆O上，所以该直线MN与圆O一定要有交点，由此可以求出m的范围．
试题解析：（1）①∵A（1，0），B（3，1），由定义可知：点A，B的“相关矩形”的底与高分别为2和1，∴点A，B的“相关矩形”的面积为2×1=2；
②由定义可知：AC是点A，C的“相关矩形”的对角线，又∵点A，C的“相关矩形”为正方形，∴直线AC与x轴的夹角为45°，设直线AC的解析为：y=x+m或y=﹣x+n，把（1，0）分别y=x+m，∴m=﹣1，∴直线AC的解析为：y=x﹣1，把（1，0）代入y=﹣x+n，∴n=1，∴y=﹣x+1，综上所述，若点A，C的“相关矩形”为正方形，直线AC的表达式为y=x﹣1或y=﹣x+1；
（2）设直线MN的解析式为y=kx+b，∵点M，N的“相关矩形”为正方形，∴由定义可知：直线MN与x轴的夹角为45°，∴k=±1，∵点N在⊙O上，∴当直线MN与⊙O有交点时，点M，N的“相关矩形”为正方形，当k=1时，作⊙O的切线AD和BC，且与直线MN平行，其中A、C为⊙O的切点，直线AD与y轴交于点D，直线BC与y轴交于点B，连接OA，OC，把M（m，3）代入y=x+b，∴b=3﹣m，∴直线MN的解析式为：y=x+3﹣m．∵∠ADO=45°，∠OAD=90°，∴OD=
OA=2，∴D（0，2）；
同理可得：B（0，﹣2），∴令x=0代入y=x+3﹣m，∴y=3﹣m，∴﹣2≤3﹣m≤2，∴1≤m≤5，当k=﹣1时，把M（m，3）代入y=﹣x+b，∴b=3+m，∴直线MN的解析式为：y=x+3+m，同理可得：﹣2≤3+m≤2，∴﹣5≤m≤﹣1；
综上所述，当点M，N的“相关矩形”为正方形时，m的取值范围是：1≤m≤5或﹣5≤m≤﹣1．
