题目内容
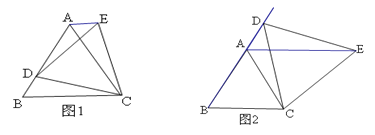
【题目】(1)如图1,D是等边三角形△ABC边BA上任意一点(D与A、B不重合),连接DC,以DC为边在BC边上方作等边三角形△DCE,连接AE,∠ABC与∠EAC有怎样数量关系直接写出结论
(2)如图2,D是等边三角形△ABC边BA延长线上一点,连接DC,以DC为边在BC边上方作等边三角形△DCE,连接AE,求证:∠ABC=∠EAC.
【答案】(1)∠ABC=∠EAC;(2)见解析
【解析】试题分析:(1)根据等边三角形的性质得到AB=AC,CD=CE,∠ACB=∠DCE=60°,利用SAS可证明△BCD≌△ACE,继而得出结论;
(2)同(1)的方法判断出△BCD≌△ACE即可;
试题解析:
(1) 证明:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
∵在△BCD和△ACE中,

∴△BCD≌△ACE(SAS),
∴∠ABC=∠EAC;
故答案为:∠ABC=∠EAC;
(2)解:结论∠ABC=∠EAC仍成立;
理由如下:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,

∴△BCD≌△ACE(SAS),
∴∠ABC=∠EAC.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目