题目内容
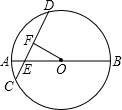 如图,⊙O的直径AB和弦CD相交于点E,AE=1cm,EB=5cm,∠DEB=60°,OF⊥CD于F.
如图,⊙O的直径AB和弦CD相交于点E,AE=1cm,EB=5cm,∠DEB=60°,OF⊥CD于F.(1)求EF的长;
(2)求CD的长.
分析:(1)根据AE=1cm,EB=5cm求出⊙O的直径,进而求出⊙O的半径,从而求出OE的长,再在Rt△EOF中,利用三角函数求出EF的长;
(2)设出CE的长,又知道EF的长,根据垂径定理表示出DF的长,从而得到CE、DE的长度表达式,再根据相交弦定理解答.
(2)设出CE的长,又知道EF的长,根据垂径定理表示出DF的长,从而得到CE、DE的长度表达式,再根据相交弦定理解答.
解答:解:(1)∵AE=1cm,EB=5cm,
∴AB=1+5=6cm,
AO=
×6=3cm,
∴EO=3-1=2cm.
又∵∠DEB=60°,
∴EF=EO•cos60°=2×
=1cm.
(2)∵OF⊥CD,
∴CF=DF,
设CE=x,
则CF=DF=x+EF=x+1,
根据相交弦定理,AE•EB=CE•ED,
x(1+x+1)=1×5,
解得:x=-1±
,
由于CE为正数,所以x=-1+
,
所以CD=2×(-1+
+1)=2
.
∴AB=1+5=6cm,
AO=
| 1 |
| 2 |
∴EO=3-1=2cm.
又∵∠DEB=60°,
∴EF=EO•cos60°=2×
| 1 |
| 2 |
(2)∵OF⊥CD,
∴CF=DF,
设CE=x,
则CF=DF=x+EF=x+1,
根据相交弦定理,AE•EB=CE•ED,
x(1+x+1)=1×5,
解得:x=-1±
| 6 |
由于CE为正数,所以x=-1+
| 6 |
所以CD=2×(-1+
| 6 |
| 6 |
点评:此题将相交弦定理和垂径定理结合起来,在解答时还要注意作出弦心距,构造直角三角形,利用三角函数求出相关线段,以便于解答.

练习册系列答案
相关题目
 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E,
 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是