题目内容
 (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=| 9 | 2 |
(1)求OD、OC的长;
(2)求证:△DOC∽△OBC;
(3)求证:CD是⊙O切线.
分析:(1)由AB的长求出OA与OB的长,根据AD,BC为圆的切线,利用切线的性质得到三角形AOD与三角形BOC都为直角三角形,利用勾股定理即可求出OD与OC的长;
(2)过D作DE垂直于BC,可得出BE=AD,DE=AB,在直角三角形DEC中,利用勾股定理求出CD的长,根据三边对应成比例的三角形相似即可得证;
(3)过O作OF垂直于CD,根据(2)中两三角形相似,利用相似三角形的对应角相等得到一对角相等,利用AAS得到三角形OCF与三角形OCB全等,由全等三角形的对应边相等得到OF=OB,即OF为圆的半径,即可确定出CD为圆O的切线.
(2)过D作DE垂直于BC,可得出BE=AD,DE=AB,在直角三角形DEC中,利用勾股定理求出CD的长,根据三边对应成比例的三角形相似即可得证;
(3)过O作OF垂直于CD,根据(2)中两三角形相似,利用相似三角形的对应角相等得到一对角相等,利用AAS得到三角形OCF与三角形OCB全等,由全等三角形的对应边相等得到OF=OB,即OF为圆的半径,即可确定出CD为圆O的切线.
解答: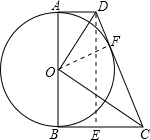 (1)解:∵AD、BC是⊙O的两条切线,
(1)解:∵AD、BC是⊙O的两条切线,
∴∠OAD=∠OBC=90°,
在Rt△AOD与Rt△BOC中,OA=OB=3,AD=2,BC=
,
根据勾股定理得:OD=
=
,OC=
=
;
(2)证明:过D作DE⊥BC,可得出∠DAB=∠ABE=∠BED=90°,
∴四边形ABED为矩形,
∴BE=AD=2,DE=AB=6,EC=BC-BE=
,
在Rt△EDC中,根据勾股定理得:DC=
=
,
∵
=
=
=
,
∴△DOC∽△OBC;
(3)证明:过O作OF⊥DC,交DC于点F,
∵△DOC∽△OBC,
∴∠BCO=∠FCO,
∵在△BCO和△FCO中,
,
∴△BCO≌△FCO(AAS),
∴OB=OF,
则CD是⊙O切线.
 (1)解:∵AD、BC是⊙O的两条切线,
(1)解:∵AD、BC是⊙O的两条切线,∴∠OAD=∠OBC=90°,
在Rt△AOD与Rt△BOC中,OA=OB=3,AD=2,BC=
| 9 |
| 2 |
根据勾股定理得:OD=
| OA2+AD2 |
| 13 |
| OB2+BC2 |
3
| ||
| 2 |
(2)证明:过D作DE⊥BC,可得出∠DAB=∠ABE=∠BED=90°,
∴四边形ABED为矩形,
∴BE=AD=2,DE=AB=6,EC=BC-BE=
| 5 |
| 2 |
在Rt△EDC中,根据勾股定理得:DC=
| DE2+EC2 |
| 13 |
| 2 |
∵
| OD |
| OB |
| OC |
| CB |
| DC |
| OC |
| ||
| 3 |
∴△DOC∽△OBC;
(3)证明:过O作OF⊥DC,交DC于点F,
∵△DOC∽△OBC,
∴∠BCO=∠FCO,
∵在△BCO和△FCO中,
|
∴△BCO≌△FCO(AAS),
∴OB=OF,
则CD是⊙O切线.
点评:此题考查了切线的判定与性质,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•柳州)如图是经过轴对称变换后所得的图形,与原图形相比( )
(2013•柳州)如图是经过轴对称变换后所得的图形,与原图形相比( )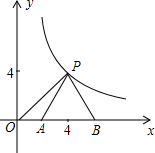 (2013•柳州)如图,点P(a,a)是反比例函数y=
(2013•柳州)如图,点P(a,a)是反比例函数y=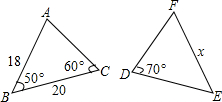 (2013•柳州)如图,△ABC≌△DEF,请根据图中提供的信息,写出x=
(2013•柳州)如图,△ABC≌△DEF,请根据图中提供的信息,写出x=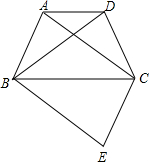 (2013•柳州)如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(2013•柳州)如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.