题目内容
 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于点F.
(1)求证:BF是⊙O的切线;
(2)连接BC,若⊙O的半径为5,∠BCD=38°,求线段BF、BC的长.(精确到0.1)
分析:(1)由垂径定理可证AB⊥CD,由CD∥BF,得AB⊥BF,则BF是⊙O的切线;
(2)连接AC,由垂径定理可知
=
,则∠CAB=∠DAB=∠BCD=38°,而AB=10,分别解直角三角形求线段BF、BC的长.
(2)连接AC,由垂径定理可知
 |
| BC |
 |
| BD |
解答:(1)证明:∵直径AB平分弦CD,
∴AB⊥CD(2分)
∵CD∥BF,
∴AB⊥BF(3分)
∴BF是⊙O的切线;(4分)
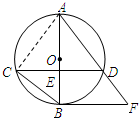
(2)解:解法一:连接AC,∵AB是⊙O的直径,
∴AB=5×2=10,∠BCA=90°
又∵AB⊥CD,
∴弧BC=弧BD,
∴∠BAC=∠BAF=∠BCD=38°(6分)
在Rt△ABF中,tan∠BAF=
,BF=AB×tan∠BAF=10×tan38°≈7.8(8分)
在Rt△ABC中,sin∠BAC=
,
∴BC=AB×sin∠BAD=10×sin38°≈6.2(10分)
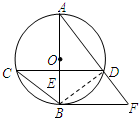
解法二:连接BD,∵AB是⊙O的直径,
∴AB=5×2=10,∠BDA=90°
又∵AB⊥CD,
∴弧BC=弧BD,
∴BC=BD,∠BAD=∠BCD=38°(6分)
在Rt△ABF中,tan∠BAF=
,
∴BF=AB×tan∠BAF=10×tan38°≈7.8(8分)
在Rt△ABD中,sin∠BAD=
,
∴BC=BD=AB×sin∠BAD=10×sin38°≈6.2.(10分)
∴AB⊥CD(2分)
∵CD∥BF,
∴AB⊥BF(3分)
∴BF是⊙O的切线;(4分)

(2)解:解法一:连接AC,∵AB是⊙O的直径,
∴AB=5×2=10,∠BCA=90°
又∵AB⊥CD,
∴弧BC=弧BD,
∴∠BAC=∠BAF=∠BCD=38°(6分)
在Rt△ABF中,tan∠BAF=
| BF |
| AB |
在Rt△ABC中,sin∠BAC=
| BC |
| AB |
∴BC=AB×sin∠BAD=10×sin38°≈6.2(10分)

解法二:连接BD,∵AB是⊙O的直径,
∴AB=5×2=10,∠BDA=90°
又∵AB⊥CD,
∴弧BC=弧BD,
∴BC=BD,∠BAD=∠BCD=38°(6分)
在Rt△ABF中,tan∠BAF=
| BF |
| AB |
∴BF=AB×tan∠BAF=10×tan38°≈7.8(8分)
在Rt△ABD中,sin∠BAD=
| BD |
| AB |
∴BC=BD=AB×sin∠BAD=10×sin38°≈6.2.(10分)
点评:本题考查了切线的判定与性质,垂径定理,圆周角定理,解直角三角形的知识.关键是利用圆周角定理将已知角进行转化,利用直径证明直角三角形.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E, 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是