Question

已知：如图，⊙O的直径AB与弦CD相交于E，

BC

=

BD

，⊙O的切线BF与弦AD的延长线相交于点F．
（1）求证：CD∥BF．
（2）连接BC，若⊙O的半径为4，cos∠BCD=

3

4

，求线段AD、CD的长．

Answer 1

分析：（1）根据

BC

=

BD

，运用垂径定理的推论得到AB⊥CD；根据切线的性质定理得到AB⊥BE，从而证明平行；
（2）根据圆周角定理得到∠A=∠C．根据直径所对的圆周角是直角，得到直角△ABD．再结合锐角三角函数的概念求解．

解答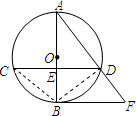：（1）证明：∵直径AB平分

CD

，
∴AB⊥CD．
∵BF与⊙O相切，AB是⊙O的直径，
∴AB⊥BF．
∴CD∥BF．

（2）解：连接BD，BC．
∵AB是⊙O的直径，
∴∠ADB=90°．
在Rt△ADB中，
∵cos∠BAF=cos∠BCD=

3

4

，AB=4×2=8．
∴AD=AB•cos∠BAF=8×

3

4

=6．
∵AB⊥CD于E，
在Rt△AED中，cos∠BAF=cos∠BCD=

3

4

，sin∠BAF=

7

4

．
∴DE=AD•sin∠BAF=6×

7

4

=

3

2

7

．
∵直径AB平分

CD

，
∴CD=2DE=3

7

．

点评：熟练运用垂径定理的推论、切线的性质定理、圆周角定理及其推论．能够利用锐角三角函数的知识解直角三角形．