题目内容
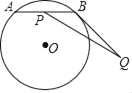
【题目】如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得![]() 的长度是
的长度是![]() ,
,![]() 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
A. 3![]() B. 2
B. 2![]() C. 9 D. 10
C. 9 D. 10
【答案】C
【解析】
连接OP,OB,O′点为OB的中点,如图,先利用弧长公式计算出⊙O的半径为2,再利用垂径定理得到OP⊥AB,则∠OPB=90°,于是利用圆周角定理得到点P在以OB为直径的圆上,直线QO′交⊙O′于E、F,如图,根据切线的性质得到OB⊥PQ,则利用勾股定理可计算出O′Q=![]() ,利用点与圆的位置关系得到m=
,利用点与圆的位置关系得到m=![]() +1,n=
+1,n=![]() -1,然后计算mn即可.
-1,然后计算mn即可.
连接OP,OB,O′点为OB的中点,如图,
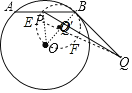
设⊙O的半径为r,
根据题意得![]() π,解得r=2,
π,解得r=2,
∵P点为AB的中点,
∴OP⊥AB,
∴∠OPB=90°,
∴点P在以OB为直径的圆上,
直线QO′交⊙O′于E、F,如图,
∴BQ为切线,
∴OB⊥PQ,
在Rt△O′BQ中,O′Q=![]() =
=![]() ,
,
∴QE=![]() +1,QF=
+1,QF=![]() -1,
-1,
即m=![]() +1,n=
+1,n=![]() -1,
-1,
∴mn=(![]() +1)(
+1)(![]() -1)=10-1=9.
-1)=10-1=9.
故选C.

练习册系列答案
相关题目