题目内容
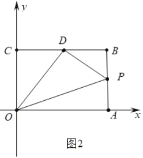
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).
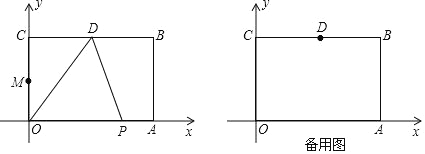
(1)①点D的坐标是(___,___)；
②当点P在AB上运动时,点P的坐标是(___,___)(用t表示)；
(2)写出△POD的面积S与t之间的函数关系式，并求出△POD的面积等于9时点P的坐标；
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=___秒.(直接写出参考答案)
【答案】（1）①D(3,4)；② P(6, t6)；（2）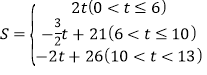
，当P(4.5,0)或(6,2)时，△POD的面积为9；（3）4.
【解析】
(1)①利用矩形的性质求出B、C两点坐标,再利用中点坐标公式计算即可;
②点P在线段AB上,求出PA即可;
(2)分三种情形分别讨论求解即可;
(3)根据,构建方程即可解决问题
(1)①∵四边形OABC是矩形,A(6,0),B(6,4)，
∴C(0,4)，
∵D是BC的中点，
∴D(3,4).
②当P在AB上运动时,P(6,t6)，
故答案为3，4，6，t6；
(2)①当0<t6时,P(t,0)，
S=
×t×4=2t.
②当6<t10时，
S=S矩形OCBAS△OPAS△PBDS△CDO=2412×6×(t6)12×3×(10t)6=
t+21，
③当10<t<13时,P(16t,4)，PD=13t，
∴S=×(13t)×4=2t+26，
综上所述,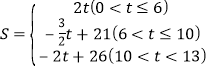
.
若S=9，由①得到2t=9，t=4.5，
∴P1(4.5,0)，
若S=9,由②得到,t+21=9，即t=8，
∴P2(6,2).
若S=9,由③得到,2t+26=9,t=
(不合题意舍弃)，
综上所述,当P(4.5,0)或(6,2)时，△POD的面积为9.
(3)如图4中，
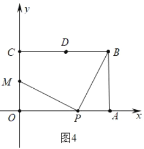
∵OM=CM=2，PM=PB，OP=t，
∴22+t2=42+(6t)2，
解得t=4.
∴将线段BP绕点P逆时针旋转，点B恰好落到OC的中点M处，则此时点P运动的时间t=4s，
故答案为4.
