Question

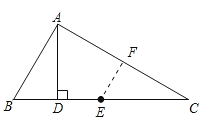
【题目】如图，梯形ABCD中，AD∥BC ， ∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，若BC=7，MN=3，则EF为（　　）
A.3
B.4
C.5
D.6

Answer 1

【答案】B
【解析】解答：过点M分别作G∥AB ， MH∥CD ，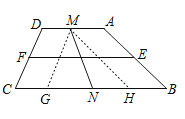
得平行四边形ABHM和平行四边形DCGM ，
∴∠NGM+∠NHM=∠B+∠C=90°，GH=BC-AD ， MG=MH
∴GH=2MN=6（直角三角形斜边上的中线等于斜边的一半）
∴AD=7-6=1
∴EF=4，
故选B.
分析：过点N分别作NG∥AB ， NH∥CD ， 得平行四边形ABGN和平行四边形DCHN ， 根据平行四边形的性质可得到△GNH为直角三角形，且MN为其斜边上的中线，由已知可求得AD的长，从而不难求中位线的长了 ．
【考点精析】通过灵活运用梯形的中位线，掌握梯形的中位线平行于梯形的两底并等于两底和的一半即可以解答此题．