Question

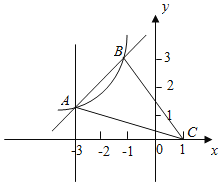
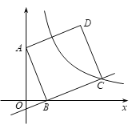
【题目】如图，在直角坐标系中，正方形ABCD绕点A（0，6）旋转，当点B落在x轴上时，点C刚好落在反比例函数（k≠0，x＞0)的图像上．已知sin∠OAB＝.

（1）求反比例函数的表达式；

（2）反比例函数的图像是否经过AD边的中点，并说明理由．

Answer 1

【答案】（1）；（2） 不经过AD边的中点，理由见解析;

【解析】

（1）过C点作CE⊥x轴于E，如图，利用正弦的定义得到sin∠OAB=，设OB=，则AB=5，利用勾股定理即可求得，接着证明△AOB≌△BEC得到AO=BE，OB=CE，从而得到C的坐标，然后利用待定系数法求反比例函数解析式；
（2）利用平移的方法确定D点坐标，再利用线段中点坐标公式得到线段AD的中点坐标，然后根据反比例函数图象上点的坐标特征判断反比例函数的图象是否经过AD边的中点．

（1）过C点作CE⊥x轴于E，如图，

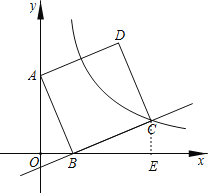
∵A（0，6），
∴OA=6，
在Rt△OAB中，sin∠OAB=，

设OB=，则AB=5，

∴OA=，

∴，

解得：，即OB=，

∴点B的坐标为(3，0)，

∵四边形ABCD为正方形，
∴BA=BC，∠ABC=90°，
∴∠ABO+∠CBE=90°，
而∠ABO+∠OAB=90°，
∴∠OAB=∠CBE，
∵∠AOB=∠BEC，∠OAB=∠CBE=90°，AB=BC，
∴△AOB≌△BEC（AAS），
∴AO=BE=6，OB=CE=3，

∴点C的坐标为(9，3)，

∵点C在反比例函数的图象上，
∴，

∴反比例函数的表达式为；

（2）反比例函数的图象不经过AD边的中点．

理由如下：
∵点B向左平移3个单位，再向上平移6个单位得到A点，

∴点C向左平移3个单位，再向上平移6个单位得到D点，

∴D点坐标为(6，9)，

∴线段AD的中点坐标为(，)，即(3，3.5)，

∵当x=3时，，

∴反比例函数图像不经过AD边的中点．