��Ŀ����
����Ŀ���������عˣ�
�α��о���������λ�����ʵķ���
��֪����ͼ�٣� ��֪![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �����е㣮
�����е㣮
��֤��![]() ��
��![]()
֤�����ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() �� ����
�� ����![]() ����֤��
����֤��![]() ��������
��������
�ɴ˵õ��ı���![]() Ϊƽ���ı��Σ� �����õ���֤����
Ϊƽ���ı��Σ� �����õ���֤����
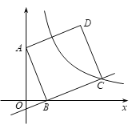
��1�����������֤�����̣���������������⣺
����ͼ��������֤�����������ĸ����ߣ�����![]() Ǧ���������ߣ���
Ǧ���������ߣ���
����֤������������д���ɣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��ѡ�� .
��ѡ�� .
��������չ��
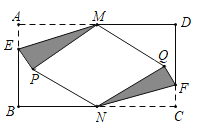
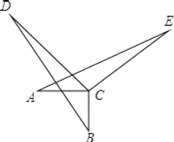
��2����ͼ�ڣ��ڵȱ�![]() �У� ��
�� ��![]() ������
������![]() ��һ���㣨��
��һ���㣨��![]() �ڵ�
�ڵ�![]() ���Ҳࣩ�����߶�
���Ҳࣩ�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ����
����![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��
�������ж��߶�![]() ��
��![]() ��������ϵ��������֤����
��������ϵ��������֤����
����![]() �����߶�
�����߶�![]() ���ȵ���Сֵ��
���ȵ���Сֵ��
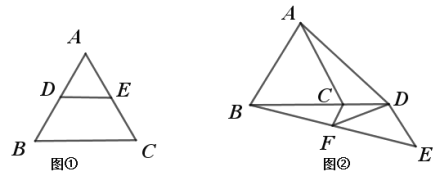
���𰸡��������عˡ���1������ͼ��������֤�����������ĸ����ߣ�����������![]() ����2����
����2����![]() ��֤�������������߶�
��֤�������������߶�![]() ���ȵ���СֵΪ
���ȵ���СֵΪ![]() ��
��
��������
��1���ٸ������⻭���������ɣ�
�������֪�ж�ȫ�ȵ�������![]() ��
��
��2�����ӳ�![]() ����
����![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() ��֤��
��֤��![]() ���õ�
���õ�![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ���ɵõ�
���ɵõ�![]() Ϊ�ȱ������Σ����Ƴ�
Ϊ�ȱ������Σ����Ƴ�![]() Ϊ�ȱ������Σ��õ�
Ϊ�ȱ������Σ��õ�![]() ��
��
������![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������������
������������![]() ����
����![]() ����������
Ϊ���������Σ�![]() ���õ�
���õ�![]() ���ɵ�
���ɵ�![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���е㣬�õ�
���е㣬�õ�![]() ����
����![]() ʱ��
ʱ��![]() ��̣���
��̣���![]() �У�
��![]() ��
��![]() ��
��
��1������ͼ��������֤�����������ĸ�������ͼ��ʾ��
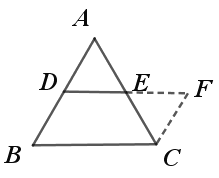
��![]() ��
��
��2����![]() ��
��
�ӳ�![]() ����
����![]() ��ʹ��
��ʹ��![]() ��
��
����![]() ��
��![]() ��
��
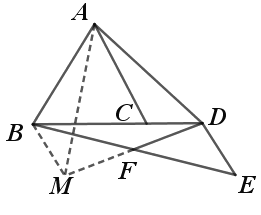
![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
![]() ��
�� ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
![]() ��
��
������![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������������
������������![]() ��
��
![]() ����������
����������![]() ��
��
![]() ��
��
![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
![]() ��
��
![]() ��
��
![]() ��
��![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ����
����![]() ��
��
��![]() ʱ��
ʱ��![]() ��̣�
��̣�
![]() ��
��
![]() ��
��
��![]() ��
�У�
![]() ��
��
![]() ��
��
���߶�![]() ���ȵ���СֵΪ
���ȵ���СֵΪ![]() ��
��