ЬтФПФкШн
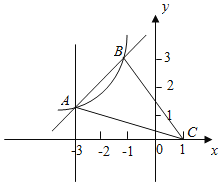
ЁОЬтФПЁПШчЭМЃЌдкЦНУцСЂНЧзјБъЯЕжаЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЌxЃМ0ЃЉгывЛДЮКЏЪ§yЃНax+bЕФЭМЯѓНЛгкЕуA(Љ3ЃЌ1)ЁЂB(mЃЌ3)ЃЎЕуCЕФзјБъЮЊ(1ЃЌ0)ЃЌСЌНгACЃЌBCЃЎ
ЃЈkЁй0ЃЌxЃМ0ЃЉгывЛДЮКЏЪ§yЃНax+bЕФЭМЯѓНЛгкЕуA(Љ3ЃЌ1)ЁЂB(mЃЌ3)ЃЎЕуCЕФзјБъЮЊ(1ЃЌ0)ЃЌСЌНгACЃЌBCЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕБxЃМ0ЪБЃЌжБНгаДГіВЛЕШЪН![]() Ёнax+bЕФНтМЏЁЁ ЁЁЃЛ
Ёнax+bЕФНтМЏЁЁ ЁЁЃЛ
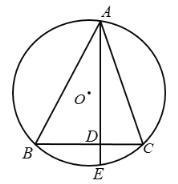
ЃЈ3ЃЉШєЕуMЮЊyжсЕФе§АыжсЩЯЕФЖЏЕуЃЌЕБЁїACMЪЧжБНЧШ§НЧаЮЪБЃЌжБНгаДГіЕуMЕФзјБъЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() ЃЌyЃНx+4ЃЛЃЈ2ЃЉЉ1ЁмxЃМ0ЛђxЁмЉ3ЃЛЃЈ3ЃЉ(0ЃЌ13)Лђ(0ЃЌ
ЃЌyЃНx+4ЃЛЃЈ2ЃЉЉ1ЁмxЃМ0ЛђxЁмЉ3ЃЛЃЈ3ЃЉ(0ЃЌ13)Лђ(0ЃЌ![]() )
)
ЁОНтЮіЁП
ЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЙлВьКЏЪ§ЭМЯѓМДПЩЧѓНтЃЛ
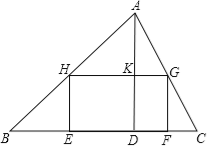
ЃЈ3ЃЉЗжMCЪЧаББпЁЂCAЪЧаББпЁЂAMЪЧаББпШ§жжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉНЋЕуAЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНЕУЃК1ЃН![]() ЃЌНтЕУЃКkЃНЉ3ЃЌ
ЃЌНтЕУЃКkЃНЉ3ЃЌ
НЋЕуBЕФзјБъДњШыЗДБШР§КЏЪ§БэДяЪНВЂНтЕУЃКmЃНЉ1ЃЌЙЪЕуBЃЈЉ1ЃЌ3ЃЉЃЌ
НЋЕуAЁЂBЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЕУЃК ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЙЪЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФБэДяЪНЗжБ№ЮЊЃКyЃНЉ![]() ЃЌyЃНx+4ЃЛ
ЃЌyЃНx+4ЃЛ
ЃЈ2ЃЉЙлВьКЏЪ§ЭМЯѓЕУЃЌЕБxЃМ0ЪБЃЌxЁнЉ1ЛђxЁмЉ3ЪБЃЌВЛЕШЪН![]() Ёнax+bГЩСЂЃЌ
Ёнax+bГЩСЂЃЌ
МДВЛЕШЪНЕФНтМЏЮЊЃКЉ1ЁмxЃМ0ЛђxЁмЉ3ЃЌ
ЙЪД№АИЮЊЃКЉ1ЁмxЃМ0ЛђxЁмЉ3ЃЛ
ЃЈ3ЃЉЩшЕуMЃЈ0ЃЌmЃЉЃЈmЃО0ЃЉЃЌЕуCЃЈ1ЃЌ0ЃЉЁЂAЃЈЉ3ЃЌ1ЃЉЃЌ
дђMC2ЃН1+m2ЃЌCA2ЃНЃЈ1+3ЃЉ2+1ЃН17ЃЌAM2ЃН9+ЃЈmЉ1ЃЉ2ЃЌ
ЕБMCЪЧаББпЪБЃЌдђ1+m2ЃН17+9+ЃЈmЉ1ЃЉ2ЃЌНтЕУЃКmЃН13ЃЛ
ЕБCAЪЧаББпЪБЃЌЭЌРэПЩЕУЃКmЃН![]() ЃЈИКжЕвбЩсШЅЃЉЃЛ
ЃЈИКжЕвбЩсШЅЃЉЃЛ
ЕБAMЪЧаББпЪБЃЌЭЌРэПЩЕУЃКmЃНЉ4ЃЈЩсШЅЃЉЃЛ
ЙЪД№АИЮЊЃЈ0ЃЌ13ЃЉЛђЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

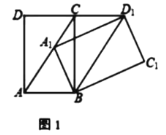
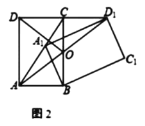
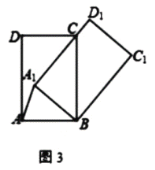
ЁОЬтФПЁПНёФъЪЧЭбЦЖЙЅМсОіЪЄжЎФъЃЌЮвЪаФГЯчЮЊСЫдіМгХЉУёЪеШыЃЌОіЖЈРћгУЕБЕигХжЪЩНСжЭСЕизЪдДЗЂеЙдАСжТЬЛЏЪїУчХрг§ВњвЕЃЎЧАЦкгЩЯчХЉММеОв§НјЁАвјагЁБЁЂЁАТоККЫЩЁБЁЂЁАЙугёРМЁБЁЂЁАжёАиЁБЫФИіЦЗжжЙВ![]() ПУгзУчНјааЪдг§ГЩУчЪЕбщЃЌВЂАбЪЕбщЪ§ОнЛцжЦГЩЯТЭМЫљЪОЕФЩШаЮЭГМЦЭМКЭВЛЭъећЕФЬѕаЮЭГМЦЭМЃЌвбжЊЪЕбщжажёАиЕФГЩУчТЪЪЧ
ПУгзУчНјааЪдг§ГЩУчЪЕбщЃЌВЂАбЪЕбщЪ§ОнЛцжЦГЩЯТЭМЫљЪОЕФЩШаЮЭГМЦЭМКЭВЛЭъећЕФЬѕаЮЭГМЦЭМЃЌвбжЊЪЕбщжажёАиЕФГЩУчТЪЪЧ![]() ЃЎ
ЃЎ
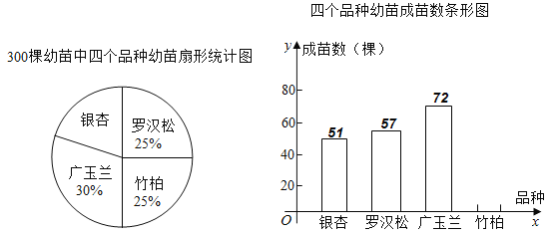
ЃЈ1ЃЉЧыФуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉШчЙћДгет![]() ПУЪЕбщгзУчжаЫцЛњГщШЁвЛПУгзУчЃЌЧѓЫќФмГЩУчЕФИХТЪЃЛ
ПУЪЕбщгзУчжаЫцЛњГщШЁвЛПУгзУчЃЌЧѓЫќФмГЩУчЕФИХТЪЃЛ
ЃЈ3ЃЉИљОнЪаГЁЕїВщЃЌетЫФИіЦЗжжЕФЪїУчЕФгзУчНјМлЁЂГЩУчЪлМлКЭЪаГЁашЧѓШчЯТБэЫљЪОЃК
ЪїУчЦЗжж | вјаг | ТоККЫЩ | ЙугёРМ | жёАи |
УППУгзУчНјМлЃЈдЊЃЉ |
|
|
|
|
УППУГЩУчЪлМлЃЈдЊЃЉ |
|
|
|
|
ЪаГЁашЧѓЃЈЭђПУЃЉ |
|
|
|
|
МйЩшГ§СЫЙКТђгзУчЭтЃЌХрг§УППУГЩУчЛЙашЗЪСЯЕШжЇГі![]() дЊЃЈЮДГЩЙІХрг§ГЩГЩУчЕФДЫЯюжЇГіКіТдВЛМЦЃЉЃЌИУЯчИљОнЪаГЁашЧѓзщжЏ
дЊЃЈЮДГЩЙІХрг§ГЩГЩУчЕФДЫЯюжЇГіКіТдВЛМЦЃЉЃЌИУЯчИљОнЪаГЁашЧѓзщжЏ![]() ДхХЉУёХрг§вјагЪїУчКЭТоККЫЩЪїУчВЂНЋШЋВПГЩУчЯњЪлЭъГЩКѓЃЌПЩЮЊБОЯч
ДхХЉУёХрг§вјагЪїУчКЭТоККЫЩЪїУчВЂНЋШЋВПГЩУчЯњЪлЭъГЩКѓЃЌПЩЮЊБОЯч![]() ДхХЉУёдіМгЪеШыЖрЩйЭђдЊЃП
ДхХЉУёдіМгЪеШыЖрЩйЭђдЊЃП