题目内容
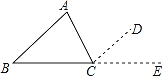
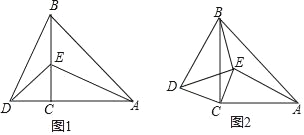
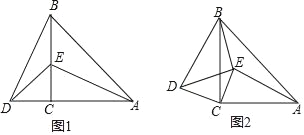
【题目】△DCE和△ABC是一大一小两块等腰三角尺,∠DCE=∠ACB=90°,AC=BC,EC=DC.
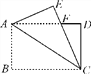
(1)如图1所示,若∠DBE=28°,试求∠AEB的大小;
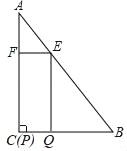
(2)若将△DCE绕C点顺时针旋转到图2所示,∠DBE=n°,试求∠AEB的大小.(用含n的式子表示)
【答案】(1)∠AEB=118°;(2)∠AEB=90°+n°.
【解析】
(1)依据DCE=∠ACB=90°,AC=BC,EC=DC,即可判定△BCD≌△ACE,再根据三角形外角性质,即可得到∠AEB的大小;
(2)先根据∠DCE=∠ACB=90°,AC=BC,EC=DC,判定△BCD≌△ACE,即可得到∠DBC=∠EAC,再根据三角形内角和定理,即可得到∠AEB的大小.
(1)如图1,∵∠DCE=∠ACB=90°,AC=BC,EC=DC,
∴△BCD≌△ACE,
∴∠DBC=∠EAC=28°,
∵∠AEB是△ACE的外角,
∴∠AEB=∠ACE+∠EAC=90°+28°=118°;
(2)如图2,∵∠DCE=∠ACB=90°,AC=BC,EC=DC,
∴∠BCD=∠ACE,
∴△BCD≌△ACE,
∴∠DBC=∠EAC,
∵∠DBE=∠DBC+∠CBE=n°,
∴∠CAE+∠CBE=n°,
又∵∠ABC+∠BAC=90°,
∴∠ABE+∠BAE=90°﹣n°,
∴△AEB中,∠AEB=180°﹣(∠ABE+∠BAE)=180°﹣(90°﹣n°)=90°+n°.

练习册系列答案
相关题目