ΧβΡΩΡΎ»ί
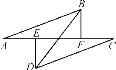
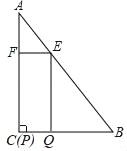
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœAΘΫ30ΓψΘ§ΓœCΘΫ90ΓψΘ§ABΘΫ12Θ§ΥΡ±Ώ–ΈEFPQ «ΨΊ–ΈΘ§ΒψP”κΒψC÷ΊΚœΘ§ΒψQΓΔEΓΔFΖ÷±π‘ΎBCΓΔABΓΔAC…œΘ®ΒψE”κΒψAΓΔΒψBΨυ≤Μ÷ΊΚœΘ©Θ°
Θ®1Θ©Β±AEΘΫ8 ±Θ§«σEFΒΡ≥ΛΘΜ
Θ®2Θ©…ηAEΘΫxΘ§ΨΊ–ΈEFPQΒΡΟφΜΐΈΣyΘ°
ΔΌ«σy”κxΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎΒ±xΈΣΚΈ÷Β ±Θ§y”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «Εύ…ΌΘΩ
Θ®3Θ©Β±ΨΊ–ΈEFPQΒΡΟφΜΐΉν¥σ ±Θ§ΫΪΨΊ–ΈEFPQ“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»―Ί…δœΏCB‘»ΥΌœρ”“‘ΥΕ·Θ®Β±ΒψPΒΫ¥οΒψB ±ΆΘ÷Ι‘ΥΕ·Θ©Θ§…η‘ΥΕ· ±ΦδΈΣtΟκΘ§ΨΊ–ΈEFPQ”κΓςABC÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§«σS”κtΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©4ΘΜΘ®2Θ©ΔΌy=©¹![]() x2+3
x2+3![]() xΘ®0ΘΦxΘΦ12Θ©ΘΜΔΎx=6 ±Θ§y”–Ήν¥σ÷ΒΈΣ9
xΘ®0ΘΦxΘΦ12Θ©ΘΜΔΎx=6 ±Θ§y”–Ήν¥σ÷ΒΈΣ9![]() ΘΜΘ®3Θ©S=
ΘΜΘ®3Θ©S=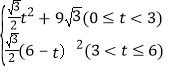
ΓΨΫβΈωΓΩ
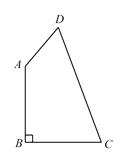
(1)”…EFΓΈBC,Ω…ΒΟ![]() ,”…¥ΥΦ¥Ω…ΫβΨωΈ Χβ;
,”…¥ΥΦ¥Ω…ΫβΨωΈ Χβ;
(2)ΔΌœ»ΗυΨίΒψEΈΣAB…œ“ΜΒψΒΟ≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß,ΗυΨί30Ε»ΒΡ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ «σ≥ωEFΚΆAFΒΡ≥Λ,‘Ύ‘ΎRtΓςACB÷–,ΗυΨί»ΐΫ«Κ· ΐ«σ≥ωACΒΡ≥Λ,ΦΤΥψFCΒΡ≥Λ,άϊ”ΟΨΊ–ΈΒΡΟφΜΐΙΪ ΫΩ…«σΒΟSΒΡΚ· ΐΙΊœΒ Ϋ;
ΔΎΑ―Εΰ¥ΈΚ· ΐΒΡΙΊœΒ Ϋ≈δΖΫΩ…“‘ΒΟΫα¬έ;
(3)Ζ÷ΝΫ÷÷«ι–ΈΖ÷±π«σΫβΦ¥Ω…ΫβΨωΈ Χβ.
ΫβΘΚΘ®1Θ©‘ΎRtΓςABC÷–Θ§ΓΏAB=12Θ§ΓœA=30ΓψΘ§
ΓύBC=![]() AB=6Θ§AC=
AB=6Θ§AC=![]() BC=6
BC=6![]() Θ§
Θ§
ΓΏΥΡ±Ώ–ΈEFPQ «ΨΊ–ΈΘ§
ΓύEFΓΈBCΘ§
Γύ![]() =
=![]() Θ§
Θ§
Γύ![]() =
=![]() Θ§
Θ§
ΓύEF=4Θ°
Θ®2Θ©ΔΌΓΏAB=12Θ§AE=xΘ§ΒψE”κΒψAΓΔΒψBΨυ≤Μ÷ΊΚœΘ§
Γύ0ΘΦxΘΦ12Θ§
ΓΏΥΡ±Ώ–ΈCDEF «ΨΊ–ΈΘ§
ΓύEFΓΈBCΘ§ΓœCFE=90ΓψΘ§
ΓύΓœAFE=90ΓψΘ§
‘ΎRtΓςAFE÷–Θ§ΓœA=30ΓψΘ§
ΓύEF=![]() xΘ§
xȧ
AF=cos30ΓψAE=![]() xΘ§
xȧ
‘ΎRtΓςACB÷–Θ§AB=12Θ§
Γύcos30Γψ=![]() Θ§
Θ§
ΓύAC=12ΓΝ![]() =6
=6![]() Θ§
Θ§
ΓύFC=AC©¹AF=6![]() ©¹
©¹![]() xΘ§
xȧ
Γύy=FCEF=![]() xΘ®6
xΘ®6![]() ©¹
©¹![]() xΘ©=©¹
xΘ©=©¹![]() x2+3
x2+3![]() xΘ®0ΘΦxΘΦ12Θ©ΘΜ
xΘ®0ΘΦxΘΦ12Θ©ΘΜ
ΔΎy=![]() xΘ®12©¹xΘ©=©¹
xΘ®12©¹xΘ©=©¹![]() Θ®x©¹6Θ©2+9
Θ®x©¹6Θ©2+9![]() Θ§
Θ§
Β±x=6 ±Θ§S”–Ήν¥σ÷ΒΈΣ9![]() ΘΜ
ΘΜ
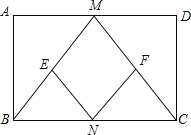
Θ®3Θ©ΔΌΒ±0ΓήtΘΦ3 ±Θ§»γΆΦ1÷–Θ§÷ΊΒΰ≤ΩΖ÷ «Έε±Ώ–ΈMFPQNΘ§
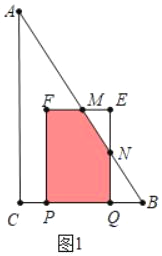
S=SΨΊ–ΈEFPQ©¹SΓςEMN=9![]() ©¹
©¹![]() t2=©¹
t2=©¹![]() t2+9
t2+9![]() Θ°
Θ°
ΔΎΒ±3ΓήtΓή6 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΓςPBNΘ§
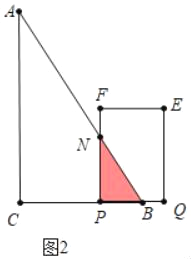
S=![]() Θ®6©¹tΘ©2Θ§
Θ®6©¹tΘ©2Θ§
Ήέ…œΥυ ωΘ§S=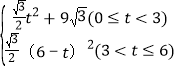

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ