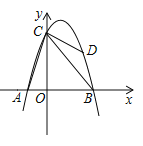ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψOΈΣΉχ±ξ‘≠ΒψΘ§÷±œΏyΘΫ©¹x+3ΫΜx÷α”ΎΒψBΘ§ΫΜy÷α”ΎΒψAΘ§ΙΐΒψAΉςACΓΆABΫΜx÷α”ΎΒψCΘ°
Θ®1Θ©»γΆΦ1Θ§«σ÷±œΏACΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ2Θ§ΒψP‘ΎAOΒΡ―”≥ΛœΏ…œΘ§ΒψQ‘ΎAC…œΘ§Ν§Ϋ”PBΘ§PQΘ§«“PQΘΫPBΘ§…ηΒψPΒΡΉίΉχ±ξΈΣtΘ§AQΒΡ≥ΛΈΣdΘ§«σd”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ®≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘ©ΘΜ
Θ®3Θ©»γΆΦ3Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§PQΫΜx÷α”ΎΒψDΘ§―”≥ΛPQΫΜBAΒΡ―”≥ΛœΏ”ΎΒψEΘ§ΙΐΒψEΉςEFΓΆPEΫΜy÷α”ΎΒψFΘ§»τDEΘΫ![]() EFΘ§«σΒψQΒΡΉχ±ξΘ°
EFΘ§«σΒψQΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ACΒΡΫβΈω ΫΈΣyΘΫx+3ΘΜΘ®2Θ©dΘΫ©¹![]() tΘΜΘ®3Θ©Θ®©¹1Θ§2Θ©
tΘΜΘ®3Θ©Θ®©¹1Θ§2Θ©
ΓΨΫβΈωΓΩ
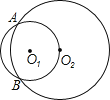
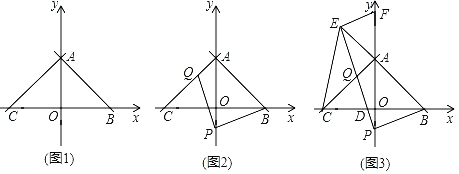
Θ®1Θ©œ»ΗυΨί÷±œΏ![]() «σ≥ωΒψAΓΔBΒΡΉχ±ξΘ§¥”ΕχΩ…ΒΟOAΓΔOBΒΡ≥ΛΘ§‘ΌΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ≈–Ε®”κ–‘÷ ΒΟ≥ωOCΒΡ≥ΛΘ§¥”ΕχΩ…ΒΟΒψCΒΡΉχ±ξΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΫβΦ¥Ω…ΘΜ
«σ≥ωΒψAΓΔBΒΡΉχ±ξΘ§¥”ΕχΩ…ΒΟOAΓΔOBΒΡ≥ΛΘ§‘ΌΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ≈–Ε®”κ–‘÷ ΒΟ≥ωOCΒΡ≥ΛΘ§¥”ΕχΩ…ΒΟΒψCΒΡΉχ±ξΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©œ»«σ≥ωΒψPΒΡΉχ±ξΘ§‘ΌΗυΨίAQΒΡ≥ΛΓΔ÷±œΏACΒΡΫβΈω ΫΩ…«σ≥ωΒψQΒΡΉχ±ξΘ§»ΜΚσΗυΨί![]() Θ§άϊ”ΟΝΫΒψ÷°ΦδΒΡΨύάκΙΪ ΫΫ®ΝΔΒ» Ϋ«σΫβΦ¥Ω…ΘΜ
Θ§άϊ”ΟΝΫΒψ÷°ΦδΒΡΨύάκΙΪ ΫΫ®ΝΔΒ» Ϋ«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©»γΆΦΘ®ΦϊΫβΈωΘ©Θ§œ»«σ≥ωΒψQΒΡΉχ±ξΘ§¥”ΕχΒΟ≥ωPNΓΔQNΒΡ≥ΛΘ§‘ΌΗυΨί’ΐ«–»ΐΫ«–ΈΚ· ΐ÷ΒΓΔΙ¥Ι…Ε®άμΒΟ≥ωDPΒΡ≥ΛΚΆ![]() Θ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏPQΒΡΫβΈω ΫΘ§ΝΣΝΔ÷±œΏABΒΡΫβΈω Ϋ«σ≥ωΒψEΒΡΉχ±ξΘ§ΉνΚσάϊ”ΟΝΫΒψ÷°ΦδΒΡΨύάκΙΪ Ϋ«σ≥ωDEΒΡ≥ΛΘ§¥ζ»κ«σΫβΦ¥Ω…Θ°
Θ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏPQΒΡΫβΈω ΫΘ§ΝΣΝΔ÷±œΏABΒΡΫβΈω Ϋ«σ≥ωΒψEΒΡΉχ±ξΘ§ΉνΚσάϊ”ΟΝΫΒψ÷°ΦδΒΡΨύάκΙΪ Ϋ«σ≥ωDEΒΡ≥ΛΘ§¥ζ»κ«σΫβΦ¥Ω…Θ°
Θ®1Θ©ΓΏ![]() ΫΜx÷α”ΎΒψBΘ§ΫΜy÷α”ΎΒψA
ΫΜx÷α”ΎΒψBΘ§ΫΜy÷α”ΎΒψA
Νν![]() Θ§‘ρ
Θ§‘ρ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]()
Γύ![]()
Νν![]() Θ§‘ρ
Θ§‘ρ![]()
Γύ![]()
ΓΏ![]() Θ§
Θ§
Γύ![]()
ΓΏ![]()
![]()
Γύ![]()
![]()
Γύ![]()
…ηACΒΡΫβΈω ΫΈΣ![]()
ΫΪΒψ![]() Θ§
Θ§![]() ¥ζ»κΒΟ
¥ζ»κΒΟ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]()
‘ρ÷±œΏACΒΡΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΓΏΒψP‘ΎAOΒΡ―”≥ΛœΏ…œΘ§ΒψPΒΡΉίΉχ±ξΈΣt
Γύ![]() Θ§
Θ§![]()
»γΆΦΘ§ΙΐΒψQΉς![]() ÷αΫΜ”ΎΒψM
÷αΫΜ”ΎΒψM
ΓΏAQΒΡ≥ΛΈΣ![]() Θ§
Θ§![]()
Γύ![]()
Γύ![]()
ΓΏ![]()
Γύ![]()
’ϊάμΒΟ![]()
ΫβΒΟ![]() Μρ
Μρ![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
Ι d”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣ![]() ΘΜ
ΘΜ
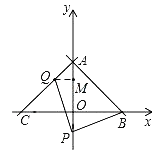
Θ®3Θ©»γΆΦΘ§ΙΐΒψQΉς![]() ÷αΫΜ”ΎΒψNΘ§‘ρ
÷αΫΜ”ΎΒψNΘ§‘ρ![]()
ΓΏ![]()
![]()
Γύ![]() Θ§
Θ§![]()
Γύ![]()
Γύ![]() Θ§Φ¥
Θ§Φ¥![]()
Γύ![]()
Γύ![]() Θ§
Θ§![]()
ΓΏ![]()
Γύ![]()
![]()
![]()
Γύ![]()
Γύ![]()
…η÷±œΏPQΒΡΫβΈω ΫΈΣ![]()
ΫΪΒψ![]() ¥ζ»κΒΟ
¥ζ»κΒΟ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ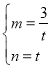
‘ρ÷±œΏPQΒΡΫβΈω ΫΈΣ![]()
ΝΣΝΔ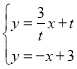 Θ§ΫβΒΟ
Θ§ΫβΒΟ![]()
Γύ![]()
![]()
”…ΝΫΒψ÷°ΦδΒΡΨύάκΙΪ ΫΒΟΘΚ![]()
ΫΪDEΓΔDPΒΡ÷Β¥ζ»κ![]() ΒΟΘΚ
ΒΟΘΚ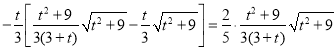
’ϊάμΒΟΘΚ![]()
ΫβΒΟ![]() Μρ
Μρ![]() Θ®≤ΜΖϊΧβ“βΘ§…α»ΞΘ©
Θ®≤ΜΖϊΧβ“βΘ§…α»ΞΘ©
![]() Θ°
Θ°