Question

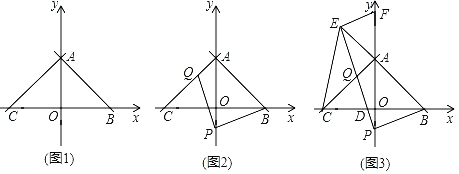
【题目】已知：如图，⊙O1和⊙O2相交于A、B两点， ⊙O1经过点O2，点C在上运动（点C 不与A、B重合），AC的延长线交⊙O2于P，连结AB、BC、BP；

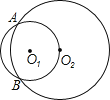
（1）按题意将图形补充完整；

（2）当点C在上运动时，图中不变的角有 （将符合要求的角都写上）

（3）线段BC、PC的长度存在何种关系？写出结论，并加以证明；

（4）设⊙O1和⊙O2的半径为、，当，满足什么条件时，为等腰直角三角形？

Answer 1

【答案】（1）见解析；（2）∠ACB，∠BCP，∠APB，∠CBP；（3）CB = CP；理由见解析；（4）

【解析】

（1）根据题意作图即可；

（2）由圆周角定理得∠ACB和∠APB不变，然后根据邻补角的性质和三角形外角的性质可得∠BCP和∠CBP不变；

（3）连结AO2，BO2，根据圆周角定理和三角形外角的性质求出∠CBP =∠P即可得BC = PC；

（4）由△BCP为等腰直角三角形得出弦AB为⊙O1的直径，△AO2B为等腰直角三角形，然后根据勾股定理列式计算即可．

解：（1）如图所示：

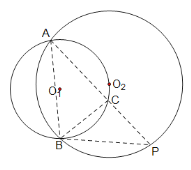
（2）由圆周角定理得：∠ACB和∠APB不变，

∴∠BCP不变，

∵∠ACB＝∠APB＋∠CBP，

∴∠CBP不变，

故图中不变的角有∠ACB，∠BCP，∠APB，∠CBP；

（3）BC = PC；

证明：连结AO2，BO2，

∵∠AO2B =∠ACB = 2∠P，∠ACB = ∠CBP +∠P，

∴∠CBP =∠P，

∴BC = PC；

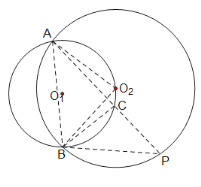
（4）要使△BCP为等腰直角三角形，已有BC＝PC，只需∠BCP =90°，

∴∠ACB＝90°，

∴弦AB为⊙O1的直径，

∴△AO2B为等腰直角三角形，

∴，

∴．